正文
運用集團展開的方法,可把實際氣體的壓強p展成密度ρ的冪級數,而冪級數的各個係數用位形空間中的某些積分來表示。
對於粒子間存在相互作用的系統,使用統計方法時最主要的是要計算巨配分函式
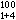 中的位形積分
中的位形積分 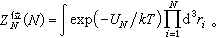
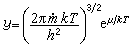 稱為經典易逸度,μ是化學勢,k和 h分別是玻耳茲曼常數和普朗克常數,T是熱力學溫度,UN是N個粒子系統的總勢能,
稱為經典易逸度,μ是化學勢,k和 h分別是玻耳茲曼常數和普朗克常數,T是熱力學溫度,UN是N個粒子系統的總勢能,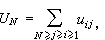 uij是兩個粒子之間的相互作用勢能。當粒子之間的距離rij →∞時,uij比
uij是兩個粒子之間的相互作用勢能。當粒子之間的距離rij →∞時,uij比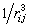 更快地趨於零,而exp(-uij/kT)則變為1。
更快地趨於零,而exp(-uij/kT)則變為1。 引入邁爾函式fij:
fij=f(rij)=exp(-uij/kT)-1,
可得: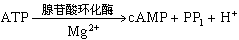
例如當N=3時,exp(-U3/kT)的圖示法是
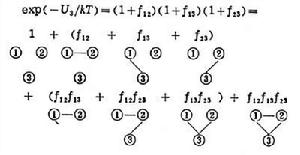 集團展開
集團展開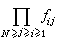 。每個圖形由一個集團或若干個集團組成。exp(-UN/kT)展開式中的每一項都對應於把代表N個粒子的N個點以一定方式分組為若干個集團,若在某種分組中,一個點的集團有m1個,二個點的集團有m2個,…l個點的集團有ml個等等,所有這些ml應滿足關係
。每個圖形由一個集團或若干個集團組成。exp(-UN/kT)展開式中的每一項都對應於把代表N個粒子的N個點以一定方式分組為若干個集團,若在某種分組中,一個點的集團有m1個,二個點的集團有m2個,…l個點的集團有ml個等等,所有這些ml應滿足關係 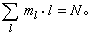
 同時每個exp(-Ul/kT)對Л個粒子坐標的積分是相同的。由於每一Л點的集團中的Л個粒子可從N個粒子中任選,排列組合滿足上式的固定一套{ml}分組的分法共有
同時每個exp(-Ul/kT)對Л個粒子坐標的積分是相同的。由於每一Л點的集團中的Л個粒子可從N個粒子中任選,排列組合滿足上式的固定一套{ml}分組的分法共有 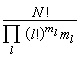

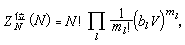
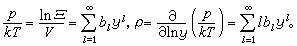
此外,B.卡恩和G.E.烏倫貝克建立了量子統計力學的集團展開法。
參考書目
J.梅逸、M.G.梅逸著,陳成琳等譯:《統計力學》,高等教育出版社,北京,1957。(J.Mayer and M.G.Mayer,Statistical Mechanics,Wiley, New York,1946.)
Kerson Huang,Statistical Mechanics, John Wiley & Sons,New York, London,1963.