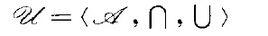簡介
集合域是一種常見的集合代數,若=<,∩,∪>是集合環,且當A∈,B∈,B⊇A時,B-A∈則稱該集合環為集合域,記為<,∩,∪,->。
這裡差“-”並不是域上的二元運算,因為當A∈,B∈,A⊈B時,不要求B-A∈。
性質
集合的域有下列性質:
1、集合域一定是集合環;
2、對於任一非空集族,存在一個包含它的最小域。只要求出包含的最小集合環=<,∩,∪>,考慮中的每一遞降集列M⊇M⊇...構造有限差鏈M=(M-M)+(M-M)+(M-M)+...+(M-M)。所有這些差鏈M的集合設為,則<,∩,∪,->是包含的最小域。
3、在集合環=<,∩,∪>中,若凡小於箇中的元素的交都在中,則所有中元素作成的長度小於的差鏈構成一個域。
4、若<,∩,∪,->是一個集合域,則∅∈。
集合環
(ring of sets)
集合環簡稱集環,是一種常見的集合代數。如果由集合構成的非空族R滿足:A∈R和B∈R蘊涵A∪B ∈R,A-B∈R,則稱R為一個集環。如果它還滿足A∈R(n=1,2,…)蘊涵∪ An∈R,則稱R為σ(集)環。如果把兩個集合的對稱差看作和,把兩個集合的交看作積,則上面定義的集環就是在這兩種運算下的代數意義上的環。對任何集合X,它的一切有限子集構成的族S是一個集環。左閉右開區間的一切有限並構成一個集環。設C是由集合X的一些子集構成的一個族,則一切包含C的集環(或σ環)的交是包含C的最小集環(或σ環),稱為由C生成的集環(或σ環)。