基本介紹
 隨機誤差項
隨機誤差項 隨機誤差項
隨機誤差項 隨機誤差項
隨機誤差項 隨機誤差項
隨機誤差項 隨機誤差項
隨機誤差項 隨機誤差項
隨機誤差項 隨機誤差項
隨機誤差項 隨機誤差項
隨機誤差項經濟計量模型由具體的方程式所組成的隨機的經濟數學模型。方程式為: ,式中 代表某種商品的需求量, 代表居民個人可支配收入。 和 稱為“ 經濟變數”,即用以描述經濟活動或經濟現象的數量特徵和數值變化的量。在式中,變數Y稱為“ 被解釋變數”,其數值的變化是因為模型中其他變數(X)的變化而引起的;變數X稱為“ 解釋變數”,其數值的變化不依賴於模型中其他變數的變化,而是自己獨立進行的。式中 和 稱為“ 參數”,它們是表示模型中變數之間數量關係的常係數。參數將各種變數連線在模型中,具體表明解釋變數對被解釋變數的影響程度。式中 稱為“ 隨機擾動項”,也稱“ 隨機誤差項”表明各種隨機因素對模型的影響,反映了未納入模型中的其他各種因素的影響。經濟計量模型就是由有關的變數、相應的參數、隨機擾動項組成的數學表達式,藉以反映經濟變數之間的因果相關關係。
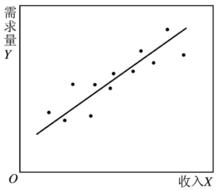 圖1
圖1 隨機誤差項
隨機誤差項 隨機誤差項
隨機誤差項如果我們蒐集到了變數 和變數 的歷史統計數據(實際值),就可以用一定的方法計算出上述模型的參數a和b。對模型參數的計算稱為“ 參數估計”。常用的估計模型參數的方法是“ 最小二乘法”。這種方法可使最終由模型計算出來的被解釋變數的估計值與其實際值之差的平方和為最小,也就是可使最終由模型計算出來的被解釋變數的估計值更接近其實際值。圖中給出了解釋變數X在不同水平上相對應的被解釋變數Y的若干實際值的數據點。圖中的直線就是由參數估計後的模型計算出來的被解釋變數Y隨解釋變數X變化的估計值所連成的直線。這條直線擬合了原來的實際值,也就是說,將被解釋變數原來的實際值在平均的意義上回歸到一條估計值的直線上。這種將變數之間的因果相關關係定量地描述出來的分析方法稱為“ 回歸分析”。為回歸分析而設定的經濟計量模型稱為“ 回歸模型”。判斷回歸模型的估計值與被解釋變數實際值的回歸擬合程度的指標稱為“ 判定係數”或“ 可決係數”。判定係數介於0和1之間,越接近於1,表明回歸模型的擬合程度越好。變數和參數均以線性的形式來表達的回歸模型稱為“ 線性回歸模型”。只含有一個解釋變數的線性回歸模型稱為“ 一元線性回歸模型”或“ 簡單線性回歸模型”。在一個方程式中含有一個以上的解釋變數的線性回歸模型稱為“ 多元線性回歸模型”。在多元線性回歸模型中,各個解釋變數之間不能存線上性相關關係。如果一個解釋變數與其他解釋變數之間存在著線性相關關係,則稱該模型具有“ 多重共線性”。這將影響對模型參數估計的準確性。因此在建立多元線性回歸模型時,在解釋變數的選取上要避免出現多重共線性問題。只用一個方程式來描述經濟關係中一個被解釋變數變化的模型稱為“ 單方程模型”。利用兩個或兩個以上方程式來描述經濟關係中多個被解釋變數變化的模型稱為“ 多方程模型”。在解釋變數中含有當期的 內生變數的多方程模型稱為“ 聯立方程模型”。在聯立方程模型中,變數分為兩類:一類是作為被解釋變數的 內生變數,即其數值是在所設定的經濟系統的模型內決定的。內生變數是對模型進行求解所要獲得的結果。另一類是作為解釋變數的 前定變數,即其數值在模型求解之前已事先給定。前定變數包括 外生變數和 內生變數的滯後變數。 外生變數是其數值在所設定的經濟系統的模型之外來決定的變數, 滯後變數是某個變數的時間滯後量。在上述模型中,假如變數X不取當期值而取其前期值,因居民個人可支配收入的前期值對當期的商品需求量有滯後的影響,則居民個人可支配收入的前期值稱為“滯後變數”。在經濟模型中,外生變數又可分為 政策變數和 非政策變數。政策變數又稱“ 可控外生變數”,是指可由決策者控制的外生變數;非政策變數又稱“ 非可控外生變數”,是指決策者難以控制或不能控制的外生變數 。
隨機誤差存在的原因
在經濟活動中,有多種原因會引起誤差。在經濟計量模型的行為方程和技術方程中,隨機誤差項所體現的誤差,主要包括以下若干方面:
變數誤差
即由於模型所包含的變數不完全所引起的誤差。實際的經濟系統要同時客群多因素的影響,在建立模型時,最理想的作法是將所有影響因素無一遺漏地反映到模型中去。但這在實際上既不可能,又無必要。因為,要將所有因素不分主次地包羅到模型中去,勢必將使模型臃腫、龐雜,失去其抽象、概括的能力,況且由於條件的限制,實際上也準以完全把握所有的影響因素。因此,通常的作法就是從簡化出發,強調抓主要矛盾,力求使模型在儘可能反映實際經濟運行情況的前提下,包含儘可能少的經濟變數,把某些暫時尚未認識到或無法觀察計量到以及認為影響力極小的經濟變黽予以忽略。這種忽略就必然產生一定的誤差,即變數誤差。 ·
模型誤差
模型誤差,又稱擬合誤差,這是由於模型選擇不當造成的誤差。這裡有兩種情況:一是對單一方程計量模型而言,一般是依據樣本數據散點分布趨勢,選擇與其逼近的擬合方程。無論這種擬合如何逼近,終究都是一種近似,這必然存在擬合誤差,二是對聯立方程模型而言,儘管可以靠擴大模型的規模,用儘可能多的方程去描述複雜的經濟系統,但模型規模總是有限制的,必須省略一些方程,這又會造成誤差。這些來源於模型的數學表達式是否得當,方程個數是否適度等引起的誤差,統稱為模型誤差。
樣本誤差
就是由於樣品數據不準、不全而造成的計量誤差。這種誤差來源於兩個方面:一是所謂測量誤差,即在獲取變數數據的過程中, 由於數據觀察者的主觀條件或客觀因素造成的測量失真,或因收集、處理、加工原始數據的方法不同,使樣本數據不能完全真實地反映其真值;二是所謂歸併誤差,即某些反映總量的樣本數據是由若干個分量加總得到的,其中包括不同時間,不同空間或同一時點上的不同來源數據的加總歸併,在此過程中,同樣會使原始數據產生扭曲變形,造成樣本誤差。
其他原因造成的誤差
除上述誤差外,還有其他意想不到的偶然因素造成的誤差。在計量過程中,還會有計量方法的選擇而造成的估算誤差等等。
所有上述這些有形的和無形的,能定量表示的和不能定量表示的誤差,都統統歸於隨機誤差項之中,成為其生成的直接原因 。
對隨機誤差項u的若干假設
為了對包含有隨機誤差項u的行為方程或技術方程進行參數估計,就應該首先具備計量方程中內生變數、外生變數和隨機項。的觀測數據。但實際上, u是既看不見,又摸不著的多因素的綜合體,其數值是觀察不到的。因此,為了推測其數值分布規律,同時也為了簡化計量工作,在經濟計量過程中就對u作出了若干假設,賦予某些統計特性,這不僅簡化了計量工作,而且為後面參數估計中的某些推導證明提供出一些理論前提。關於對u的假定,幾乎在所有經濟計量學的著述中都有闡述,雖表達方式不盡相同,但基本內容是一致的。這裡以一元線性計量模型為例,從兩個方面分述如下。
與u有關的假定
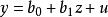 隨機誤差項
隨機誤差項這主要是對線性計量模型: 中的自變數z所作的假定,就是假定z是取值固定的隨機變數。
u自身的假定
這是對隨機項u本身所作的假定,主要的是:
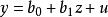 隨機誤差項
隨機誤差項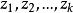 隨機誤差項
隨機誤差項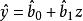 隨機誤差項
隨機誤差項假定1 u是服從常態分配的隨機變數。就是說當u是在多種隨機因素共同作用之下時, u在任意時期的取值都服從正態的機率分布。由於前已假定在一元線性計量模型中, 自變數z址非隨機變數,而因變數y卻是與u一樣是服從常態分配的,因此,可用圖1來直觀的表示出來它們之間的關係。由圖看出,對於一元線性計量模型 來說,當外生變數z取固定值 時, 由於隨機誤差u的取值機率P(u)是服從常態分配的,因而使內生變數y也是以常態分配機率取值為 。這種把u視為具有常態分配機率的假定是極重要的統計特性之一。
 圖1 u的分布示意圖
圖1 u的分布示意圖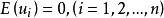 隨機誤差項
隨機誤差項假定2 u是以零為期望值的隨機變數。用數學符號表達就是 。對此假定的直觀解釋,就是對外生變數z的每一個固定值,u可以按某種機率取不同的值,但若同時考慮u的取值,則從平均意義上講,彼此之間有互相抵消的作用,使其平均值呈現以零為中心點,作幅度有限的正負波動。
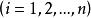 隨機誤差項
隨機誤差項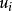 隨機誤差項
隨機誤差項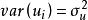 隨機誤差項
隨機誤差項 隨機誤差項
隨機誤差項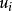 隨機誤差項
隨機誤差項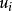 隨機誤差項
隨機誤差項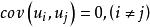 隨機誤差項
隨機誤差項 隨機誤差項
隨機誤差項假定3 u的同方差性假定。即假定對應於各次 觀察值的 ,其方差是一個常數。用數學符號表達就是 =常數。這一假定的直觀表示就是在圖1中,對應於 的取值, 的常態分配曲線其形狀相同。顯然,該假定是認為經濟過程是平穩的隨機過程,它隱含著各次觀察值,它們無論是時間序列數據,還是橫斷面資料,所顯現出來的 彼此是相互獨立的,互不影響的,用數學符號表達就是 。一般在時間序列資料中,該假定是指前後期的不隨時間而變化,保持前後期相等,故稱之為方差齊一性。將上述綜合表示出來,一般可採用如下形式:
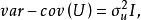 隨機誤差項
隨機誤差項 隨機誤差項
隨機誤差項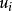 隨機誤差項
隨機誤差項 隨機誤差項
隨機誤差項式中: ——各次觀察數據隨機誤差 的列向量,即 ;
 隨機誤差項
隨機誤差項——單位向量矩陣,其階數為打X刀階,即也可表示成:
 隨機誤差項
隨機誤差項也可以表示成:
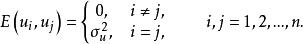 隨機誤差項
隨機誤差項 隨機誤差項
隨機誤差項綜合以上三種假設,就可對u的分布特性表述為:它是以零為期望值,以為方差的常態分配隨機變數。用數學符號表達就是:
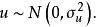 隨機誤差項
隨機誤差項假定4 u與各解釋變數即自變數無關。用數學符號表示就是:
 隨機誤差項
隨機誤差項在上述所有假定都成立的條件下,該假定是不難證明其存在性的。這是因為:
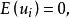 隨機誤差項
隨機誤差項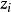 隨機誤差項
隨機誤差項已知 且為取固定值的變數,所以
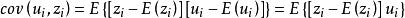 隨機誤差項
隨機誤差項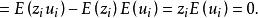 隨機誤差項
隨機誤差項這一假定在計量分析過程中也是時常用到的統計特性之一。
至於說上述這些假設是否成立,能否符合實際情況,還需再作具體分析 。

