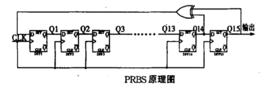
簡介
偽隨機二進制序列，是一種可以預先確定並可以重複地產生和複製，又具有隨機統計特性的二進制碼序列。在現代工程實踐中，偽隨機信號在移動通信、導航、雷達和保密通信、通信系統性能的測量等領域中有著廣泛的套用。例如，在連續波雷達中可用作測距信號，在遙控系統中可用作遙控信號，在多址通信中可用作地址信號，在數字通信中可用作群同步信號，還可用作噪聲源以及在保密通信中的加密作用等。偽隨機發生器在測距、通信等領域的套用日益受到人們重視。偽隨機信號與隨機信號的區別在於：隨機信號是不可預測的。它在將來時刻的取值只能從統計意義上去描述；偽隨機序列實質上不是隨機的，而是收發雙方都知道的確定性周期信號。之所以稱其為偽隨機序列，是因為它表現出白噪聲採樣序列的統計特性，在不知其生成方法的偵聽者看來像真的隨機序列一樣。M序列作為一種基本的PN序列，具有很強的系統性、規律性和相關性。M序列的理論發展比較成熟。實現比較簡便，利用n級移位暫存器可產生長度為2“一l的M序列。目前，3G移動通信技術仍是通信領域的研究熱點，其基本特徵之一就是碼分多址【4l，其中的碼就是PN碼，PN碼的選擇直接影響到CDMA系統的容量、抗干擾能力、接入和切換速度等性能。因此，PN碼技術作為3G移動通信系統的核心技術之一。已得到廣泛的關注、研究和套用。
在通信系統中，誤碼測試的功能和指標是其中的重要指標之一。高速PRBS的產生與再生是高速誤碼分析儀中的關鍵技術之一。在此，結合PRBS在通信系統中誤碼測試方面的套用討論由並行PRBS產生高速串列PRBS的方法 。
PRBS原理
M序列的特性
誤碼分析儀中的數碼流是偽隨機的。它實際上是一種M序列，即由帶線性反饋的移位暫存器產生的周期最長的一種序列，它具有許多特別的性質，下面只列出與M序列的有關特性。
•均衡性：在M序列的一個周期中，l和0的個數基本相等。
•遊程分布：一個序列中取值相同的那些相繼的元素合稱為一個遊程。在一個遊程中元素的個數稱為遊程長度。一般來說，在M序列中長度為k的遊程占遊程總數的1/2^k。若M序列的周期為2^n一l，那么，其中最長的遊程只有一個，即連續n個1組成的遊程是其最長的遊程。
•移位相加特性：一個M序列Mp與其經任意次延遲移位產生的另一不同序列Mr模2相加，得到的仍是Mp的某次延遲移位序列Ms。
誤碼測試的原理
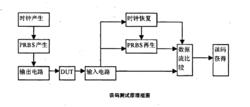
偽隨機二進制序列圖是誤碼測試的原理框圖。其中時鐘產生、PRBS產生、輸出電路等模組構成發射單元，DUT是被測電路或傳輸線路，輸入電路、時鐘恢復、PRBS再生、數據流比較、誤碼獲得等模組構成接收單元。PRBS的產生、再生是其中的關鍵技術之一。
並行PRBS產生的原理
在高速通信系統中，由於器件速度的限制，常常需要在較低的速率(如四分之一速率)下先產生並行PRBS，然後再由並/串變換電路產生高速的PRBS。
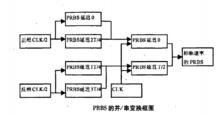
偽隨機二進制序列圖是四路並行的PRBS經過並/串變換產生指定串列速率的PRBS的過程。“CLK/2”是指需要的速率(CLK)的1/2倍的時鐘，“PRBS延遲1T/4”是指特定PRBS延遲1/4周期的PRBS。
四路(兩兩相差1/4周期的)PRBS先產生兩路1/2速率的PRBS(兩路相差1/2周期)，再由兩路相差1/2周期的PRBS產生全速率的PRBS。可見用此方法產生的PRBS，可以使其大部分電路工作在1/4速率下，在1/4速率下完成PRBS產生、誤碼插入、誤碼統計等功能；只有少數電路工作在1/2速率和全速率下。降低了對硬體的要求。
並行PRBS的實現
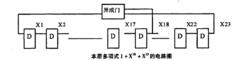
偽隨機二進制序列通信系統中使用的PRBS應符合ITU-T Rec.O.150~O.153的要求，ITU-T Rec.O.151規定周期為2^23-1的PRBS的本原多項式為1+X^18+X^23。它可以由23個D觸發器加上異或門來實現，如圖。
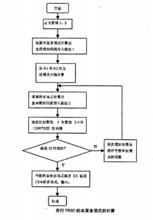
偽隨機二進制序列我們以周期為2^23-1的PRBS為例來說明四路並行的PRBS的實現。產生的四路並行的PRBS必須相差1/4個PRBS周期。。PRBS 2^23-1的周期為8388607位；其1/4周期為2097152位。X1定義為延遲0位的輸出端。依據圖提供的流程圖，可由計算機完成複雜的計算過程。設N值分別為1/4周期位(2097152位)、2/4周期位(4194304位)、3/4周期位(6291456位)，則可分別計算出延遲1T/4、2T/4、3T/4的本原多項式B、C、D
B=X^6+X^11+X^13+X^15+X^18+X^20
C=X^7+X^12+X^16+X^21
D=X^1+X^6+X^10+X^15+X^17+X^22.
PRBS的FPGA實現
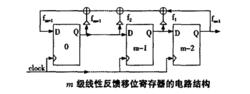
偽隨機二進制序列圖是m級線性反饋移位暫存器的電路結構。其中係數因子fi=1表示有連線，fi=0表示無連線；⊕表示異或(XOR)運算。顯然，線性反饋移位暫存器的輸出序列是有周期性的。因為一旦m個暫存器上出現了以前經歷過的狀態，則此後的狀態將周而復始。m級的線性反饋移位暫存器最多只有2m個狀態，所以重複是不可避免的。假若優個暫存器的初始狀態全為零，則線性反饋移位暫存器將一直保持全零狀態。因此，在初始狀態非全零的前提下，線性反饋移位暫存器的周期r≤2m-1。如果選取適當的反饋方式。m級線性反饋移位暫存器所產生的序列周期可以達到最大值2m-1，這時線性反饋移位暫存器所產生的偽隨機序列也稱為最長序列(或者m序列)。線性反饋移位暫存器的周期只與其反饋方式有關，而不依賴於其初始狀態。根據其反饋方式的不同，可以定義線性反饋移位暫存器的特徵多項式為：
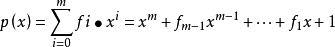偽隨機二進制序列在不同套用場合下，對線性反饋移位暫存器所產生的隨機序列的周期長度有不同要求。隨著m的增大，線性反饋移位暫存器對FPGA內部邏輯資源的消耗量線性增加，而線性反饋移位暫存器輸出的最長序列周期卻呈指數增長，這一點對實際套用來說是非常有利的。當m=63時。最大長度序列的周期可達9.22337×10^18如果CLK頻率為50MHz，則重複周期超過5800年。在大多實際套用中，這樣的序列長度是非常充裕的 。
PRBS傳送
偽隨機二進制序列利用線性反饋移位暫存器產生PRBS可以有很多種生成多項式，其中套用最廣泛的是PRBSl5序列。PRBS-15的生成多項式是：X^15+X^14+1；PRBS的生成採用FPGA內部的D觸發器(DFF)實現起來非常簡單。PRBS-15序列產生電路實現原理如圖所示。
PRBS檢測
接收端的PRBS檢測有兩種常用的方式，分別是圖案檢測和公式檢測法。
1、圖案檢測
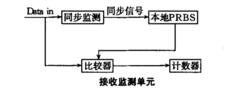
偽隨機二進制序列這種方法的方案是：在接收端同樣有一個相同的PRBS/PRss生成器，把接收到的數字序列與本地產生器輸出的碼型進行比較，從而得到誤碼的結果。在進行比較前，必須使本地的產生器要與傳送端的生成器達到同步。達到同步的原理與幀定位系統原理相似，但與後者相比要簡單的多。偽隨機序列是按一定規律(周期)產生和複製而成，所以序列的生成也存在著一定的周期，把每一周期的序列看成一個幀，由它生成的原理可知在這一周期內，每一組15位長度的碼型都是唯一存在的，可以把這15位碼型看成幀定位信號處理，從而能達到同步，只是不需要校核/保護邏輯。同步信號再控制本地生成器。原理如圖。
圖中，從遠端接收到PRBS。首先進行數據監測，監測到預設的數字則啟動本地麟產生器，這樣使接收的序列與本地的序列達到完全同步，從而便於比較，比較器是一個簡單的異或門，當兩序列數據不同時比較器輸出高電平，當相同時則為低電平。當輸出高電平則啟動計數器。從而計數器累加誤碼個數。CPU定時訪問計數暫存器，訪問後計數器清零，CPU將會計算誤碼率。
2、公式計算法
偽隨機二進制序列
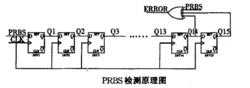
偽隨機二進制序列PRBS都是按照一定的公式生成的，所以在接收端只要驗證接收到的數字序列是否能夠滿足公式從而判斷出是否誤碼。PRBS公式驗證原理如圖所示。在這種方法中有一個現象沒有考慮到，接收來的信號全0’的情況，全‘0’情況可以驗證也滿足了上圖，所以如果Q1、Q2、……Q15同時為0時，error也要輸出高電平。如圖，從遠端接收到PRBS送入到PRBs監測端。檢測來到的數據是否符合PRBS產生的公式，如不符合則輸出脈衝送到計數器中。
3、兩種方法的比較
在前一種設計中，需要同步電路與PRBS生成器，所以它需要一段時間的同步而且資源也比較浪費，但是一旦達到同步後檢測的準確性比較高。而後一種的方法直接套用PRBS產生器的數學公式，它的同步速度快而且實現也比較簡單，節省資源。但是由檢測原理圖看出如果序列中出現一個比特的誤碼，它將會影響到對隨後序列的判斷，所以用這種方法檢測出的誤碼數偏高。
