其他形式
微分形式:
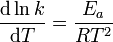阿倫尼烏斯公式定積分形式:
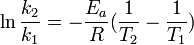阿倫尼烏斯公式
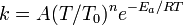阿倫尼烏斯公式阿倫尼烏斯方程一般適用於溫度變化範圍不大的情況，這時A和Ea變化不大，阿倫尼烏斯方程有很好的適用性。若溫度範圍較大，則阿倫尼烏斯方程會產生誤差，此時常用下面的公式對阿倫尼烏斯方程進行修正:其中A、n、Ea均為常數，實驗得到的n值通常在−1至1之間。如果n=0，就得到未修正的阿倫尼烏斯方程。
也可以利用下面的廣延指數式進行修正:
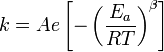阿倫尼烏斯公式其中β為無量綱量。
適用範圍
需要注意，阿倫尼烏斯經驗公式的前提假設認為活化能Ea被視為與溫度無關的常數，在一定溫度範圍內與實驗結果符合，但是由於溫度範圍較寬或是較複雜的反應，lnk與1/T就不是一條很好的直線了。說明活化能與溫度是有關的，阿倫尼烏斯經驗公式對某些 複雜反應不適用。在溫度範圍較寬的情況下，有人提出了修正的三參量 方程式加以校正： k=A（T^m）exp（-E/RT）式中A、E、m均由實驗確定。將三參量方程對T微分後代入阿倫尼烏斯公式的微分式得： Ea=E+mRT , 該式表明活化能與溫度的定量關係。一般的實驗值m較小，在溫度不太高時，阿倫尼烏斯經驗公式仍與實驗結果較好相符。
公式的推導
阿倫尼烏斯公式是由路易斯的有效碰撞理論作為前提的。
有效碰撞理論
早在1918年，路易斯運用氣體運動論的成果，提出了反應速度的碰撞理論。該理論認為，反應物分子間的碰撞是反應進行的先決條件。反應物分子碰撞的頻率的越高，反應速率越大。
下面以碘化氫氣體的分解為例，對碰撞理論進行討論。
2HI(g)----H(g)+I(g)
通過理論計算，濃度為1×10mol·L的HI氣體在973K時分子碰撞頻率約為3.5×10L·s。如果每一次碰撞都發生反應，則反應速率應約為5.8×10mol·L·s。然而實驗結果表明，在這種條件下的實際反應速率約為1.2×10mol·L·s.這個數據告訴我們，在為數眾多的碰撞中，大多數的碰撞並不能引起反應，只有極少數碰撞是有效的。
阿倫尼烏斯碰撞理論認為，碰撞中能發生一組分子（下面簡稱分子組）首先必須具備足夠的能量，以克服分子無限接近時電子云之間的斥力，從而導致分子中的原子重排，即發生化學反應。我們把具有足夠能量的分子組稱為活化分子組。活化分子組在全部分子占有的比例以及活化分子組所完成的碰撞次數占總數的比例，都是符合麥克斯韋—玻爾茲曼分布的，
故有：f=e^[-Ea/(RT)]
式中f稱為能量因子，其意義是能量滿足要求的碰撞占總碰撞次數的分數；e為自然對數的底；R為氣體常數；T為絕對溫度；Ea等於能發生有效碰撞的活化分子組所具有的最低能量的N倍（N是阿弗加德羅常數）。
能量是有效碰撞的一個必要條件，但不充分。只有當活化分子組中的各個分支採取合適的取向進行碰撞時，反應才能發生。一下面反應說明這個問題。
NO+CO----NO+CO
只有當CO分子中的碳原子與NO中的氧原子相碰時，才能發生重排反應；而碳原子與氮原子相碰的這種取向，則不會發生氧原子的轉移。
因此，真的有效碰撞次數，應該在總碰撞次數上再乘以一個校正因子，即取向因子P。
反應物分子之間在單位時間內單位體積中所發生的碰撞的總數是Na（阿弗加德羅常數）的Z倍，則平均反應速率ν可表示為
ν=ZPf=ZPe^(-Ea/RT)
