推導過程
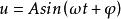 阻抗模
阻抗模對於正弦電壓
 阻抗模
阻抗模 阻抗模
阻抗模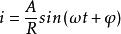 阻抗模
阻抗模當電壓加在電阻元件 兩端,設電阻為 ,產生電流 。
 阻抗模
阻抗模 阻抗模
阻抗模 阻抗模
阻抗模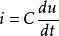 阻抗模
阻抗模當電壓加在電容元件 兩端,設電容為 ,由電容 , ,可得流經電流為
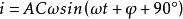 阻抗模
阻抗模 阻抗模
阻抗模 阻抗模
阻抗模 阻抗模
阻抗模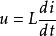 阻抗模
阻抗模當電壓加在電感元件 兩端,設電感為 ,由電感 , ,可得產生電流為
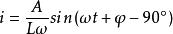 阻抗模
阻抗模 阻抗模
阻抗模 阻抗模
阻抗模 阻抗模
阻抗模由上述公式可知,電阻元件 ,電容元件 ,電感元件 均不會改變電路中正弦電壓與電流的頻率,因此可以引入相量的概念,用一個帶有幅值和角度的複數量表示正弦量,即
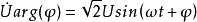 阻抗模
阻抗模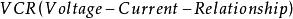 阻抗模
阻抗模則可以把電路元件 用相量形式表示,上述的表達式可以寫為
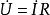 阻抗模
阻抗模電阻元件:
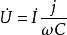 阻抗模
阻抗模電容元件:
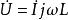 阻抗模
阻抗模電感元件:
 阻抗模
阻抗模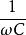 阻抗模
阻抗模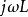 阻抗模
阻抗模 阻抗模
阻抗模 阻抗模
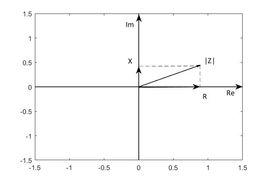
阻抗模其中,j為複數符號,為了區別於電流符號i。寫為相量形式後,採用類似電阻元件VCR的表達方法,則稱 為電容的容抗,它對應複平面上演著虛軸負方向,長度為 的相量;稱 為電感的感抗,它對應複平面上沿著虛軸正方向,長度為 的相量。容抗和感抗的單位都是歐姆(Ω),習慣上用 表示。容抗、感抗和電阻是構成阻抗的三個部分。
一般的電路元件都不僅僅有電阻或容感特性,而是兩種或三種的組合,一般將其等效為電容、電阻和電感的串聯,也可以等效為並聯。但不管用何種等效,都可以將其複平面上的相量表達為
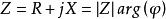 阻抗模
阻抗模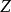 阻抗模
阻抗模 阻抗模
阻抗模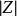 阻抗模
阻抗模稱為阻抗, 稱為阻抗的阻抗角, 就稱為阻抗模,它對應阻抗相量的長度,數學關係上有
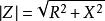 阻抗模
阻抗模工程套用
阻抗模忽略了阻抗的阻抗角,僅僅考慮其模量,等效於將阻抗相量簡化為實軸上一條等長度的相量,即將阻抗簡化為電阻。對於很多阻抗角足夠小的場合,如直流電動機電樞阻抗、變壓器阻抗,可以很大程度上簡化電機的建模。
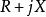 阻抗模
阻抗模以電力系統中負荷節點為例,負荷阻抗複平面上可以表示為 以坐標原點為圓心 , 以零點為半徑的右半圓 ( R>0 )。負荷阻抗位於半圓周 時 , 負荷節點處臨界狀態 ; 如果負荷阻抗位於半圓的外側時 , 負荷電壓位於高壓域 , 處於穩定狀態 ; 相反 ,如果負荷阻抗位於半圓的內側時 , 負荷電壓位於低壓域 , 電壓失穩。利用臨界阻抗模 的穩定性 , 可以用 負荷節點工作點的阻抗模與其臨界阻抗模進行比較 , 來判斷該節點的電壓穩定性 , 進而判斷全系統的 電壓穩定性。
此外,臨界阻抗模可以對網路理論中最大功率傳輸定義進行擴展:在交流網路中 , 網路對任一 負荷節點在不同功率因數條件下的最大傳輸功率條件是 ,該負荷 節點的阻抗模等於其臨界阻抗模 (戴維南等效阻抗模 ),有助於分析電壓質量。