通訊中 阻塞率的含義
在一個區域,由於經濟方面的原因,所提供的鏈路數往往比電話用戶數要少得多。當有人要打電話時,會發現所有鏈路可能全部處於繁忙狀態,我們稱這種情況為“阻塞”或“時間阻塞”。提供的鏈路越多,則系統的阻塞率越小,提供給用戶的服務質量就越好,即電話系統的承載能力決定了鏈路的數目,而鏈路的數目又決定了系統的阻塞率。
話路阻塞率的計算公式為:
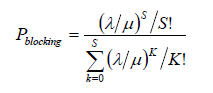
其中S 為鏈路數,λ/μ的單位是‘erl’。從物理意義上講λ/μ具有同時通話鏈路數的意義,蒲松分布中λ/μ參數的意義是某一參數出現的頻率。例如排隊事件,該參數的物理意義是單位時間佇列長度增加量的大小。再舉一個例子說明蒲松分
布的意義。
在一段時間[0,1]內,某交通路口出現事故的次數為λ。將時間段分為n 等分,n→∞,l1=[0, 1/n ],l2=[1/n, 2/n ],…。
假設1:在li 內發生一次事故的機率與時間長度成正比,而在li 內發生兩次事故的機率是不可能的。設λ為某一常數,在li 內發生交通事故的機率λ/n。
假設2:在各小段時間內,發生事故的事件相互獨立。
那么,發生i 次交通事故的機率是多少?
顯然將i 次交通事故的機率用二項分布描述。


以上分析說明了蒲松分布中各參數的意義:λ為事件發生的頻率,指數i 是指某一段時間內發生i 次同樣的事件,公式計算的是i 個事件在一段時間內發生的機率。對於有線話路中繼占用的例子,可以用蒲松分布來描述。這裡,固定時間段,定義平均每次通話時間為1/μ,將1/μ分為n 等分,每一小時間段為1/(nμ)。做相同的分析就得到:
P(x = i) = (λ μ )i e−(λ μ ) i!
當中繼線只有n 條時,i=n 的概念就是阻塞率,因此有:

這裡λ/μ就是單位時間內的Erlang 話務量。
同樣的Erl 容量的條件下,允許的阻塞率越高,需要的鏈路數越少。
