開放宇宙模型
在宇宙學原理這一前提下,解愛因斯坦引力場方程,得宇宙的動態時空度規: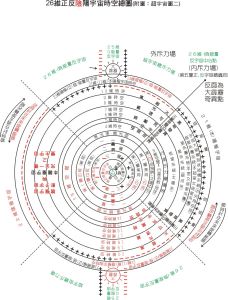 宇宙模型圖一
宇宙模型圖一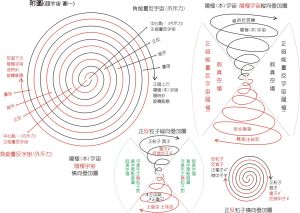 宇宙模型圖二
宇宙模型圖二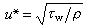 ,
,
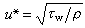
開放宇宙模型是弗里德曼宇宙模型的一個解。
 宇宙模型圖一
宇宙模型圖一 宇宙模型圖二
宇宙模型圖二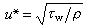 ,
,
開放宇宙(Open universe)如果一個宇宙質量不大,引力就不足以降低其膨脹速度,這就叫開放宇宙。
星系 膨脹著的宇宙 收縮宇宙 結構模型 普利高津的“開放宇宙”“量子漲落宇宙模型”是由楊志勇教授(理學博士、物理學博士後)和侯洵教授(中國科學院院士)他們兩人於2000年提出的。人們已在這一領域進行了長期大量的和卓...
具體內容 最早期 原初宇宙核 宇宙核 形成閉合宇宙模型即“弗里德曼宇宙模型”,當宇宙物質的平均密度觀測值大於臨界密度值時。宇宙不會永遠膨脹下去,而是最終要收縮為一個點。這就是閉合宇宙模型。
閉合宇宙模型 正文 配圖 相關連線多元宇宙是一個理論上的無限個或有限個可能的宇宙的集合,包括了一切存在和可能存在的事物:所有的空間、時間、物質、能量以及描述它們的物理定律和物理常數。多元...
基本概要 提出背景 發展歷程 研究現狀 研究前景宇宙是萬物的總稱,是時間和空間的統一。“宇宙”三要素為時間、空間、質量。時空質的依存關係確立了事物的演化秩序。宇宙是物質世界,不依賴於人的意志而客觀存在...
誕生 理論 膨脹 詞源考察 觀念歷史根據大爆炸宇宙論,甚早期的宇宙是一大片由微觀粒子構成的均勻氣體,溫度極高,密度極大,且以很大的速率膨脹著。這些氣體在熱平衡下有均勻的度。這統一的溫度是當...
概述 宇宙的誕生 宇宙大爆炸學 觀點提出過程 理論觀點多元宇宙是一個理論上的無限個或有限個可能的宇宙的集合,包括了一切存在和可能存在的事物:所有的空間、時間、物質、能量以及描述它們的物理定律和物理常數。多元...
基本概要 提出背景 發展歷程 研究現狀 研究前景宇宙是萬物的總稱,是時間和空間的統一。“宇宙”三要素為時間、空間、質量。時空質的依存關係確立了事物的演化秩序。宇宙是物質世界,不依賴於人的意志而客觀存在...
誕生 理論 膨脹 詞源考察 觀念歷史