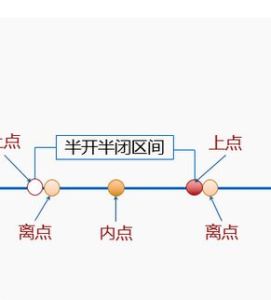
定義
邊界點是拓撲空間的基本概念之一,邊界概念是康托爾(Cantor,G.(F.P.))在研究歐幾里得空間的子集情形時首先引入的。邊界點及邊界的定義如下:
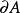 邊界點
邊界點設A是拓撲空間X的子集,x∈X,若x既不屬於A的內部,又不屬於A的外部,亦即x的任意鄰域既含有A的點也含有不屬於A的點,則稱x是A的 邊界點。A的所有邊界點組成的集合稱為A的 邊界,記為.
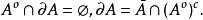 邊界點
邊界點註:將A的全部內點組成的集合記為A ,則有
舉例
例1 設A=[-1,0)∪{1/n | n∈N},則
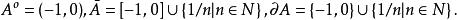 邊界點
邊界點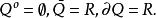 邊界點
邊界點例2 考慮有理點集Q,則
拓展
邊界點處理在數據挖掘技術中有重要意義,它們代表了一類歸屬並不明確的個體,如果單純地依靠某種方法把其歸類到一個特定的簇中,其效果往往適得其反。邊界點不同於孤立點和噪聲點。孤立點是一類在統計上處於少數地位的對象,噪聲點是一類對統計產生干擾或者偏離一定分布的對象,它們通常位於數據空間的低密區域中,而邊界點則不同,它們是數據空間中處於高密區域邊沿的一類數據對象,它們的一側是高密區域,一側是相對的低密區域。
聚類技術的研究是近幾年研究的一個熱點,已經提出的許多聚類算法,但是,對聚類邊界模式的探討還不多。聚類的邊界點是指位於高密聚類邊沿的一類數據對象,它代表了游離在兩個或多個類別之間的一類個體對象,其歸屬並不明確,它們常常具有兩個或兩個以上的聚類特徵。邊界點研究有著重要的套用價值。
Chen Xia等提出了聚類邊界點檢測算法BORDER,其邊界點的定義如下:
定義 邊界點(Boundary point):一個邊界點p是指滿足下列兩個條件的數據對象:
(1)它位於一個高密的區域IR;
(2)p的附近存在一個區域IR’,Density(IR) >> Density(IR’),或者Density(IR) << Density(IR’)。
聚類的邊界代表了一種潛在的模式,對數據挖掘的著重要的意義。但是目前涉及的邊界的算法並不多,對其的研究遠遠不夠。
在DBSCAN算法中,提到邊界點:一個非核心點對象,如果其落在某核心點的Eps-鄰域內,則稱之為邊界點。一個邊界點可能同時落入一個或多個核心點的Eps-鄰域。