簡介
 內點
內點 內點
內點 內點
內點 內點
內點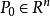 內點
內點設 E 是 n 維空間 中的一個點集, 是 中的一個定點,E包含於 , ,如果存在點P的某個鄰域U(P)∈E,則稱P為E的內點。或者也可以定義為設M∈E,如果存在M的一個δ鄰域U(M,δ),使U(M,δ)∈E,則M是E的內點。
點的類型分類
通常有兩種分類方式:
(1)分為外點、內點、邊界點。
(2)分為聚點、孤立點、外點。
外點
外點,即如果存在點P的某個鄰域U(P),使得U(P)∩E=Φ,則稱P為E的外點。
邊界點
如果點P的任一鄰域內既含有屬於E的點,又含有不屬於E的點,則稱P為E的邊界點。
聚點
設拓撲空間(X,τ),A⊆X,x∈X。若x的每個鄰域都含有A \ {x}中的點,則稱x為A的聚點。
孤立點
 內點
內點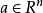 內點
內點設A是 中的一個點集,點 ,若a∈A,但a不屬於A的導集,則稱a為A的孤立點。
點之間的區別和關係
設有點集E
內點、孤立點必屬於E,外點必不屬於E,邊界點、聚點可屬於E可不屬於E。
內點:①屬於E;
②存在一個鄰域全含於E;
外點:①不屬於E;
②存在一個鄰域全含於E的補集,即存在一個鄰域∩E=∅;
邊界點:全部鄰域同時有屬於E、不屬於E的點;
聚點:全部鄰域都有E的無窮多點;
孤立點:①屬於E;
②不是聚點,即存在一個鄰域∩E={該點};
關係:
內點一定是聚點,聚點可能是內點可能是邊界點;
孤立點一定是邊界點,邊界點可能是孤立點可能是聚點。
