逐步法簡介
數學中的逐步逼近法是這樣一種方法,為了解決一個數學問題,首先從與該問題的實質內容有著本質聯繫的某些容易著手的條件或某些減弱的條件出發,再逐步地擴大(或縮小)範圍,逐步逼近,以至最後達到問題所要求的解。
逐步逼近法在解決問題的過程中,使後步比前一步更接近探索目標,其一般有三種結果:
(1)通過有限步逐步逼近最終達到目標
(2)通過無限逼近的極限,最終達到目標;
(3)不能最終達到目標,但可以通過多次的逼近,取得對目標的接近而達到一定的要求。
逐步法又稱驗誤法,是通過逐次假設求得估計殘值的現值,而取其最準確者。逐步法往往需要反覆驗證若干次,才能得到正確或較正確的答案,從而效率較差。
逐步法舉例
例1:租憑計算
以租憑利率計算為例,通過逐次試錯、推斷和修正,使以下公式成立,從而求得租賃利率,(以每期租金先付為例):
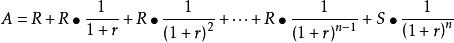 逐步法
逐步法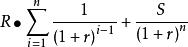 逐步法
逐步法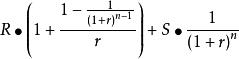 逐步法
逐步法A表示租賃開始日租賃資產的公平價值; R表示每期租金數; S表示租賃資產估計殘值; n表示租期; r表示折現率。
例2:分段問題
將一條長為n的線段AB分成n段,兩端端點染藍色,其餘分點染紅色或藍色,求證:端點被染上兩種顏色的小線段(稱為“標準線段”)有偶數條。
證:首先考慮一種特殊情形:即除端點外(已染成藍色),再將n-1個分點C(i=1,2,…,n-1)全部染藍色,這時標準線段有0條,是偶數下面再進行調整,看此量是不是不變的。
第一步,從左自右將n-1個分點中的對應前述狀態藍點的某一點該染成紅色,這時標準線段增加兩條。如下圖1所示:
 圖1
圖1第二步,將餘下的n-2個分點中的對應前述狀態任一藍點的一點染成紅色,這時標準線段或不增加,或增加兩條,,,.,9如此調整下去,每次調整標準線段或增加(減少)兩條,所以總可以調整到題設要求的一般狀態。因此,標準線段的條數是0或2的整數倍,總是偶數。如下圖二所示:
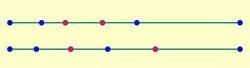 圖2
圖2補充
還有一種稱逐步淘汰逼近的方法,這種方法,是以一定的限定條件為依據,對所研究的對象進行考察丕符合條符食冬件的對象選上對象淘汰,最後得到所需求解的結果。
套用逐步淘汰逼近著名的例子莫過於公元前先把天乎2的2的蓓數划去,再把天於3的3的數划去,接著又把大於5的5的倍數划去如此划去,直至划去了在,定範圍內的所有合再划去1。正是利用這種近笨拙的杯素的逐步淘汰篩選造出了十萬以內的質數。
