逆高斯分布

逆高斯分布（Inverse Gaussian distribution）是統計學中一種常用的分布，逆高斯分布起源於有正漂移的Wiener過程或Brown運動中的首達時分布，它與機率論與統計學都有著密切的聯繫。逆高斯分布在壽命試驗、衛生科學、 精算學、生態學、昆蟲學等眾多領域得到了極為廣泛的套用，應當歸因於它所具有的十分自然、優良的機率與統計性質。

背景

基本的連續分布一般包括指數分布、常態分配、對數常態分配、截斷常態分配、Weibull分布、極值分布、Gamma分布等；實際上，分布的機率及統計理論都有一個由淺顯到深入的發展過程，對於這些分布的掌握及運用都有一個由模糊到清晰的過程，而另外一些分布的機率及統計理論和實際運用的普及與發展到相當程度時，也可以稱其為基本分布，逆高斯分布就是這樣一個分布。

定義

逆高斯分布（Inverse Gaussian distribution）是統計學中一種常用的分布，其密度函式為

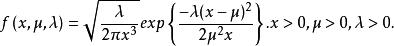逆高斯分布

該分布含有兩個參數μ和λ ，Wald分布是 μ = λ = 1 時逆高斯分布的特例。當 λ 趨近於無窮時，逆高斯分布逐漸趨近於高斯分布（即常態分配），逆高斯分布有多項類似於高斯分布的特性。“逆”可能容易引起混淆，其實它的含義是高斯分布描述的是在布朗運動中某一固定時刻的距離分布，而逆高斯分布描述的是到達固定距離所需時間的分布。

逆高斯分布圖形

其分布的大致圖形如下：

圖2.逆高斯分布圖形

相關分布

廣義逆高斯分布

廣義逆高斯分布的特徵函式為：

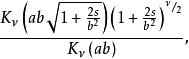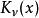逆高斯分布

逆高斯分布

（1）式中代表MacDonald函式，亦稱為第三類變換過的Bessel函式；

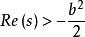逆高斯分布

（2）定義域為：；

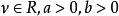逆高斯分布

（3）涉及到的參數：。

正態逆高斯分布

正態逆高斯分布的特徵函式為：

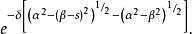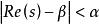逆高斯分布

逆高斯分布

（1）定義域為：；

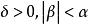逆高斯分布

（2）涉及到的參數：。