介紹
迴轉半徑(Radius of Gyration)當一力矩作用於一個物體時,物體會呈現應有的旋轉運動。物體對於一個直軸的迴轉半徑,是此物體所有粒子,對於此直軸的均方根距離。
物體對於一個直軸的迴轉半徑,是與對於此直軸的轉動慣量和物體的質量有關。
物理上認為,剛體按一定規律分布的質量,在轉動中等效於集中在某一點上的一個質點的質量,假設此點離某軸線的垂距為k,剛體對該軸線的轉動慣量與該等效質點對此同一軸線的轉動慣量相等,即I=mk^2,則k稱為該剛體對該軸線的迴轉半徑。
迴轉半徑的大小與截面的形心軸有關。最小迴轉半徑一般指非對稱截面中(如不等邊角鋼),對兩個形心軸的迴轉半徑中的較小者。這在計算構件的長細比時,如構件的平面內和平面外計算長度相等時,它的長細比就要用最小迴轉半徑計算。
迴轉半徑是動力學中的概念,迴轉半徑又稱慣性半徑。物體在轉動時對慣性的度量稱轉動慣量。它的大小等於物體各微分質量與其到轉動軸的距離平方的乘積之和。迴轉半徑是指物體微分質量假設的集中點到轉動軸間的距離,它的大小等於轉動慣量除總質量後再開平方。建築工程結構(如鋼結構等)計算中的迴轉半徑是指構件截面的迴轉半徑。它是從運動學中的轉動慣量的概念推演而來的。在構件截面中,各微分面積與其到形心軸(或座標軸)的距離平方的乘積之和稱截面的慣性矩;各微分面積的假設的集中點到形心軸(或座標軸)的距離稱為截面的迴轉半徑,它的大小等於慣性矩除總面積後再開平方。截面迴轉半徑反應了截面面積對坐標軸的聚集程度,面積分布離坐標軸越遠、,慣性矩大,其迴轉半徑也越大,反之則小!在截面面積相等的情況下,迴轉半徑大的截面其抗彎能力強。如工字鋼、槽鋼、鋼管和一些空心構件要比同樣截面面積的矩形實心構件的抗彎能力強就是這個道理。截面的迴轉半徑一般用來驗算構件穩定性能(如長細比)。
關於鋼結構近似迴轉半徑計算的研究
1 近似迴轉半徑
由於鋼材的強度高,因此只要較小的截面就能滿足較高的承載力,截面小,會導致截面不是很展開,截面過多地集中在一起會引起抗彎能力不足進而引發穩定問題,這就是鋼結構有穩定問題而混凝土沒有穩定問題的原因,鋼結構的核心問題是穩定,穩定是截面展開程度在受力的情況下的一種反應,而迴轉半徑是截面展開程度的直接度量,其計算公式為i=√I/A(其中I為繞計算軸的慣性矩,A為面積),可見迴轉半徑在鋼結構中的作用很重要。對於受壓構件(包括軸壓和壓彎)和受拉構件(包括軸拉和拉彎)而言,構件的剛度控制是由長細比來決定的,受壓構件的彎曲失穩的穩定係數也主要是由長細比來決定,對於壓彎構件,通常使用的工字形截面而言,其平面外的穩定係數主要是由對應的梁繞豎軸的長細比決定的。我們進行受壓構件的試算大概確定截面的大小時也要用到長細比,對於一定長度的構件迴轉半徑定了,長細比就定了。
結論
1,迴轉半徑僅與截面所在垂直於計算軸的軸的高度有關,也就是僅與截面在垂直於計算軸的方向上的展開程度有關,
2,迴轉半徑與構成截面的板件的厚度和寬度幾乎沒有什麼關係。
3,長方形截面為0.3,中間加一塊板變為0.2,比原來降低0.1,是因為慣性矩沒有什麼變化,但是面積有較大的增加,將中間板移到端部,則變成是0.3,比原來升高0.1,是因為慣性矩有較大的增加,將T形截面的另一端再加上一塊板件,則變成0.4,又在原來的基礎上升高0.1,這只是一個近似的規律,並且有一定的實用條件,但是對於我們通常所見的截面一般都能滿足以上規律。
物體對於一支直軸的迴轉半徑,是與對於此直軸的轉動慣量和物體的質量有關。
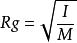 迴轉半徑
迴轉半徑特別注意,是個截面二次軸矩,不是慣性張量。

