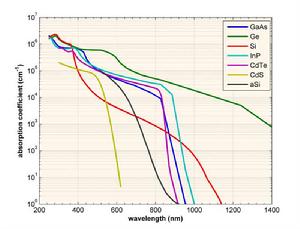
計算過程
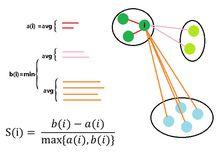 輪廓係數
輪廓係數假設我們已經通過一定算法,將待分類數據進行了聚類。常用的比如使用K-means ,將待分類數據分為了 k 個簇 。對於簇中的每個向量。分別計算它們的輪廓係數。
對於其中的一個點 i 來說:
計算 a(i) = average(i向量到所有它屬於的簇中其它點的距離)
計算 b(i) = min (i向量到各個非本身所在簇的所有點的平均距離)
那么 i 向量輪廓係數就為:
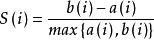 輪廓係數
輪廓係數可見輪廓係數的值是介於 [-1,1] ,越趨近於1代表內聚度和分離度都相對較優。
將所有點的輪廓係數求平均,就是該聚類結果總的輪廓係數。
a(i) :i向量到同一簇內其他點 不相似程度的平均值
b(i) :i向量到其他簇的平均 不相似程度的最小值
注意事項
上部分中所說的“距離”,指的是不相似度(區別於相似度)。“距離“值越大,代表不相似度程度越高。
歐氏距離就滿足這個條件,而Tanimoto Measure 則用做相似度度量。
當簇內只有一點時,我們定義輪廓係數s(i)為0。