定義介紹
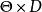 費用函式
費用函式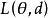 費用函式
費用函式定義在乘積空間上的函式稱為損失函式,如果它滿足如下兩個條件:
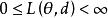 費用函式
費用函式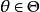 費用函式
費用函式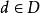 費用函式
費用函式(1)對任意的和成立;
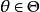 費用函式
費用函式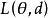 費用函式
費用函式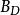 費用函式
費用函式(2)對任意固定的,作為 d 的函式是可測的。
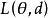 費用函式
費用函式 費用函式
費用函式 費用函式
費用函式表示當自然解處於狀態時(參數的真實值為),人們採取決策(行動)d 所造成的損失。
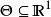 費用函式
費用函式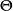 費用函式
費用函式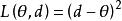 費用函式
費用函式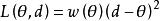 費用函式
費用函式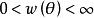 費用函式
費用函式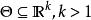 費用函式
費用函式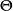 費用函式
費用函式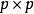 費用函式
費用函式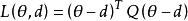 費用函式
費用函式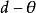 費用函式
費用函式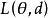 費用函式
費用函式若即是一堆實數空間上的子集,則稱形如的損失函式為平方損失函式,稱形如的損失函式為加權平方損失函式,其中。若,即是 k 維實數空間上的子集。設 Q 為的正定矩陣。則稱形如的損失函式為二次損失函式,其中 “T” 表示矩陣轉置。二次損失函式關於偏差是非對稱的損失函式稱為非對稱的損失函式。
套用
損失函式是描述系統在不同參數(parameter)值之下的損失。要套用損失的函式,其損失必須是通過某種媒介可以衡量的。損失函式在實踐中最重要的運用,在於協助我們通過過程的改善而持續減少目標值的變異,並非僅僅追求符合邏輯。
損失函式並非一定是對稱的。有時候其中一邊很陡峭,有時候則兩邊都很陡峭。舉例而言,為了使鋼片較容易焊接,需要加入鈳。但鈳的加入量如果低於必須量,純粹是浪費,對焊接一點益處都沒有。然而鈳用量如高於十萬分之一,也是一種浪費,所增加的利益相當有限。戴明博士曾在《企業研究的樣本設計》(Sample Design in Business Research)一書內,列示了一個實際的損失函式。它顯示我們只需要儘量靠近樣本的最優組合就行了,只要非常接近就可以了。
實際套用
案例一
某個工廠人員的產出,以每小時多少元來計算,而損失函式所顯示的,是產出以室內通風條件而改變的情形。廠內工作的每個人,都有自己的損失函式。為了簡化說明,假設每個人的損失函式均為一條拋物線,其底部一點代表產出值最大時的通風條件,把所有人員的損失函式進行疊加,公司整體的損失函式也必然是一條拋物線。如果通風條件偏離這個最佳水準,就會有額外損失發生。該拋物線與橫軸相切時,切點的左右各有一小段與橫軸幾近重合。也就是說,有最適點偏離一小短距離,損失小到可以忽略不計。因此,當室內通風條件稍稍偏離均衡點,發生的損失可以忽略不計。但是遠離均衡點時,總是有人必須支付這損失。如果我們能夠導出有具體數字的損失函式,我們就可以計算出最優均衡點,在均衡點中最適合的通風條件如何,以及達到要求的費用支出是多少。
案例二
以趕火車作為符合規格的例子。假設我們的時間價值為每分鐘n元,下圖左邊的斜線是損失線的斜率;早一分鐘到達月台,將讓我們損失n元,早兩分鐘到達損失2n元。另一方面,如果沒有趕上火車,我們的損失是M元。遲到半分鐘或遲到5分鐘損失一樣,損失函式直接由零跳到M。
當然問題也可複雜化,例如火車每天離站的時間也有變化,所以也可以畫出一個分配圖。火車到站時間三個標準差的界限可能是8秒。把問題這樣複雜化,對於我們了解和套用損失函式並沒有特別大的幫助,因此我們就說到這裡。 另一個例子,是參加星期日早上11點15分的禮拜時所碰到的停車問題。教堂的停車場最大負荷是停放50輛車子,但這些車位在10點50分左右仍然客滿,因為作完上一場禮拜的車主仍在喝咖啡。等他們一離開,這些空位馬上就會被排成長龍等待的車隊填滿。如果你想占到一個車位,不得不早早去排隊。那些晚到的人在這裡找不到車位,只能到街上去找,但實際上往往無功而返。所以,上策還是提早一點去等,承受等待的損失而能占到位置。
這項理論也可以套用到任何計畫的截止時間上。某人要求必須在截止日期前完成工作,萬一未能趕上這個時間,勢將使計畫延誤或出錯。為了能準時完成,可以擬定工作內容與步驟的綱要。把個步驟的截止日期 設 定一段期間要比設定為固定的從容,而且有時間作最後的修訂,可能把計畫做得更好。
