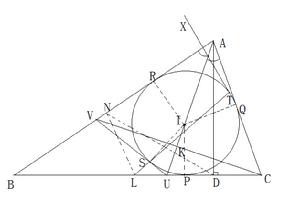
定理敘述
三角形的九點圓與其內切圓以及三個旁切圓相切。
定理證明
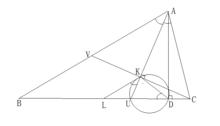
設△ABC的內心為I，九點圓的圓心為V。三邊中點分別為L，M，N，內切圓與三邊的切點分別是P，Q，R，三邊上的垂足分別為D，E，F。
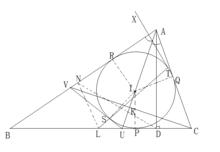全局圖不妨設AB>AC。
假設⊙I與⊙V相切於點T，那么LT與⊙I相交，設另一個交點為S。
過點S作⊙I的切線，分別交AB和BC於V，U，連線AU。
又作兩圓的公切線TX，使其與邊AB位於LT的同側。
由假設知
∠XTL=∠LDT
而TX和SV都是⊙I的切線，且與弦ST所夾的圓弧相同，於是
∠XTL=∠VST
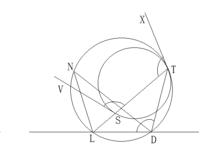局部圖1因此
∠LDT=∠VST
則
∠UDT+∠UST=180°
這就是說，S，T，D，U共圓。
而這等價於：LU×LD=LS×LT
又 LP²=LS×LT
故有 LP²=LU×LD
另一方面，T是公共的切點，自然在⊙V上，
因此 L，D，T，N共圓，進而有
∠LTD=∠LND
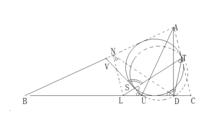局部圖2由已導出的S，T，D，U共圓，得
∠LTD=∠STD=180°-∠SUD=∠VUB
=∠AVU-∠B
而
∠LND=∠NLB-∠NDB
=∠ACB-∠NBD
=∠C-∠B
（這裡用了LN∥AC，以及直角三角形斜邊上中線等於斜邊的一半）
所以，就得到
∠AVU=∠C
注意到AV，AC，CU，UV均與⊙I相切，於是有
∠AIR=∠AIQ
∠UIS=∠UIP
∠RIS=∠QIS
三式相加，即知
∠AIU=180°
也即是說，A，I，U三點共線。
另外，AV=AC，這可由△AIV≌△AIC得到。
（這說明，公切點T可如下得到：
連線AI，並延長交BC於點U，
過點U作⊙I的切線，切點為S，交AB於V，
最後連線LS，其延長線與⊙I的交點即是所謂的公切點T。
）
連線CV，與AU交於點K，
則K是VC的中點。
前面已得到：LP²=LU×LD
而
2LP=(BL+LP)-(CL-LP)
=BP-CP
=BR-CQ
=(BR+AR)-(CQ+AQ)
=AB-AC
=AB-AV
=BV
費爾巴哈定理即 LP=BV
然而
LK是△CBV的中位線
費爾巴哈定理於是 LK=BV
因之 LP=LK
故 LK²=LU×LD
由於以上推導均可逆轉，因此我們只需證明： LK²=LU×LD。往證之
這等價於：LK與圓KUD相切
於是只需證：∠LKU=∠KDU
局部圖3再注意到 LK∥AB（LK是△CBV的中位線），即有
∠LKU=∠BAU
又AU是角平分線，於是
∠LKU=∠CAU=∠CAK
於是又只需證：∠CAK=∠KDU
即證：∠CAK+∠CDK=180°
這即是證：A，C，D，K四點共圓
由於 AK⊥KC（易得），AD⊥DC
所以 A，C，D，K確實共圓。
這就證明了⊙I與⊙V內切。
旁切圓的情形是類似的。
證畢
另略證：
OI^2=R^2-2Rr
IH^2=2r^2-2Rr'
OH^2=R^2-4Rr'(其中r‘是垂心H的垂足三角形的內切圓半徑，R、r是三角形ABC外接圓和內切圓半徑)
FI^2=1/2(OI^2+IH^2)-1/4OH^2=(1/2R-r)^2
FI=1/2R-r這就證明了九點圓與內切圓內切（九點圓半徑為外接圓半徑一半。F是九點圓圓心，I為內心）
