敘述
 開世定理
開世定理 開世定理
開世定理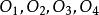 開世定理
開世定理 開世定理
開世定理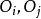 開世定理
開世定理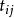 開世定理
開世定理開世定理的背景是圓的內切圓。設有半徑為 的一個圓 ,圓內又有四個圓 內切於圓 (如圖1所示)。如果將圓 的外公切線的長度設為 ,那么開世定理聲稱,有下列等式成立。
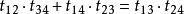 開世定理
開世定理 開世定理
開世定理可以注意到,如果四個內切的圓都退化成點的話,就會變成圓 上的四個點,而開世定理中的等式也會化為托勒密定理。
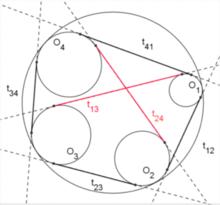 圖1
圖1證明
 開世定理
開世定理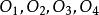 開世定理
開世定理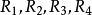 開世定理
開世定理 開世定理
開世定理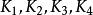 開世定理
開世定理設大圓的圓心是點 ;四個圓的圓心分別是點 ,半徑分別是 。每個圓與大圓 的切點分別是 。
首先,根據勾股定理可以推出:對於任意的i 和j,都有
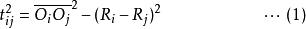 開世定理
開世定理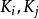 開世定理
開世定理接下來的思路是將這個公式右邊的各個長度用 來表示。
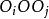 開世定理
開世定理考慮三角形 ,根據三角形的餘弦定理:
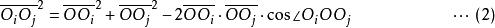 開世定理
開世定理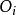 開世定理
開世定理由於每個圓 都和大圓相切,所以:
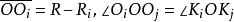 開世定理
開世定理 開世定理
開世定理 開世定理
開世定理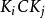 開世定理
開世定理設點 為大圓 上的任意一點,根據三角形的正弦定理,在三角形 之中,有:
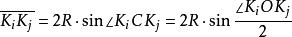 開世定理
開世定理所以,餘弦式
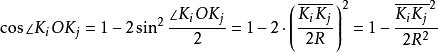 開世定理
開世定理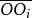 開世定理
開世定理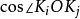 開世定理
開世定理將以上 與 代入式子(2)中,就可以得到:
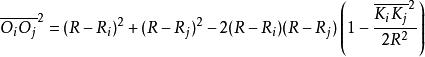 開世定理
開世定理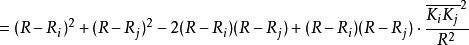 開世定理
開世定理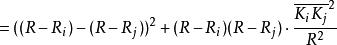 開世定理
開世定理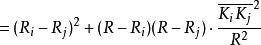 開世定理
開世定理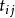 開世定理
開世定理再代入式子 (1)中,就得到 的表達式:
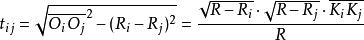 開世定理
開世定理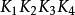 開世定理
開世定理以上等式對所有的 i和 j都成立,因此只要注意到四邊形 是圓內接四邊形,那么對其套用套用托勒密定理就可以得到開世定理:
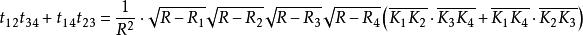 開世定理
開世定理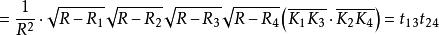 開世定理
開世定理證明完畢。
推廣
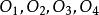 開世定理
開世定理 開世定理
開世定理可以用類似的方法證明,只要當圓與大圓相切(不論是外切還是內切),就會有類似開世定理的等式成立。這是需要註明,對任意的i 和j:
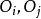 開世定理
開世定理 開世定理
開世定理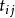 開世定理
開世定理1、如果圓是與大圓以同樣的方式相切(都是外切或者都是內切)的話,則表示兩個圓的外公切線的長度;
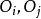 開世定理
開世定理 開世定理
開世定理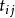 開世定理
開世定理2、如果圓是與大圓以不同的方式相切(一個是外切而另一個是內切)的話,則表示兩個圓的內公切線的長度。
另一個特點是:這定理的逆定理也成立。也就是說,如果開世定理的等式成立,那么這些圓必定以規定的方式與大圓相切。
套用
在歐幾里得幾何學中,開世定理可以用來證明多種不同的結論。比如說費爾巴哈定理的一個簡潔證明中就用到了它。
