簡介
糾纏譜(entanglement spectrum) 是一個由 Li 和 Haldane 在2008年提出的量子力學概念,可作為糾纏熵的推廣,用來分析量子多體系統的波函式。 糾纏譜的數學定義是
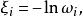 糾纏譜
糾纏譜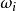 糾纏譜
糾纏譜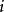 糾纏譜
糾纏譜其中 是約化密度矩陣的第 個本徵值。
糾纏熵
一個由A部分和B部分組成的量子力學的系統,A與B之間可能存在某種 遠距離的相關性,即使A與B之間並不存在互動作用力,這種關聯仍然存在,而且A部分和B部分的空間距離可以很遠,這種概念稱為 糾纏。糾纏的強弱程度常利用 糾纏熵來定量分析。事實上,糾纏的概念並不局限只把系統分成兩個部分,但是多個部分的糾纏強弱在定量分析上遭遇許多困難,目前仍物理學家研究的課題之一。常見的糾纏熵都是定義在一個由A部分和B部分組成的純態系統,例如:馮紐曼熵、仁義熵。
馮紐曼熵
馮紐曼熵(von Neumann entropy)是吉布士熵的直接推廣,約翰·馮·諾伊曼首次用來量化分析一個量子系統的熵。定義是
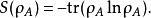 糾纏譜
糾纏譜仁義熵
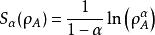 糾纏譜
糾纏譜仁義熵(Rényi entropy)的定義是 ,其中α≥0是非負實數。
波函式
在量子力學裡,量子系統的量子態可以用 波函式(英語:wave function)來描述。薛丁格方程設定波函式如何隨著時間流逝而演化。從數學角度來看,薛丁格方程乃是一種波動方程,因此,波函式具有類似波的性質。這說明了波函式這術語的命名原因。
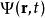 糾纏譜
糾纏譜 糾纏譜
糾纏譜 糾纏譜
糾纏譜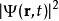 糾纏譜
糾纏譜 糾纏譜
糾纏譜 糾纏譜
糾纏譜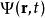 糾纏譜
糾纏譜波函式 是一種復值函式,表示粒子在位置 、時間 的機率幅,它的絕對值平方 是在位置 、時間 找到粒子的機率密度。以另一種角度詮釋,波函式 是“在某時間、某位置發生相互作用的機率幅”。
參閱
•波包
