簡介
角位移(Angular displacement)是描述物體轉動時位置變化的物理量。物體的角位移是指以特定方式圍繞指定軸鏇轉點或線的弧度(度數,轉數)的角度。 當物體圍繞其軸線鏇轉時,運動不能簡單地被分析為粒子,因為在圓周運動中,它在任何時間(t)都經歷變化的速度和加速度。 當處理對象在鏇轉時,考慮物體本身就變得更加簡單。 當所有顆粒之間的分離在整個物體運動中保持恆定時,通常認為該物體是剛性的,因此,例如其一部分質量不會飛離。 在現實的意義上,一切都可以變形,然而這種影響是微乎其微的。 因此,剛體在固定軸上的鏇轉被稱為鏇轉運動。
運動學分析
角位移
 角位移
角位移 角位移
角位移粒子以半徑r做圓周運動。 移動弧長s後,其角位置相對於其原始位置為的角度為 ,其中 。
在數學和物理學中,通常使用自然單位弧度而不是度或轉數。 單位轉換如下:
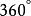 角位移
角位移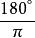 角位移
角位移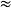 角位移
角位移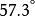 角位移
角位移1rev= =2πrad,1rad= 。
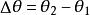 角位移
角位移角位移是角位置的變化: ,
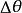 角位移
角位移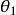 角位移
角位移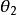 角位移
角位移其中是 角位移, 是初始角位置, 是最終的角位置。
有限大的角位移
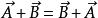 角位移
角位移有限大的角位移不是矢量,因為他不滿足交換律。兩個矢量相加,遵守平行四邊形加法所遵守的交換律。即:
一個長方體,
若先繞z軸轉90度,再繞y軸轉90度,則得到圖1所示結果。
 角位移
角位移若先繞y軸轉90度,再繞z軸轉90度,則得到圖2所示結果。
 角位移
角位移兩種情況都是繞z軸和y軸各轉了90度,只是轉動的順序不同,但是最終結果卻不同,說明不滿足交換律。由此可見,有限大的角位移不是矢量。
無限小的角位移
無限小的角位移是矢量。
角速度
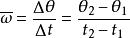 角位移
角位移 角位移
角位移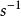 角位移
角位移瞬時角速度由下式給出,角速度是每單位時間角位移的變化。 角速度的符號是 ,單位通常為rad ,
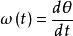 角位移
角位移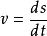 角位移
角位移使用角位置的公式並且代入 ,我們可以得到,
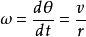 角位移
角位移其中v是粒子的平移速度,角速度和頻率相關。
角加速度
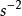 角位移
角位移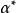 角位移
角位移變化的角速度表示在剛體中存在角加速度,通常以rad 測量。 時間間隔Δt的平均角加速度 由下式給出,
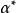 角位移
角位移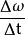 角位移
角位移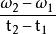 角位移
角位移= =
瞬時加速度α(t)由下式給出,
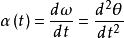 角位移
角位移因此,角加速度是角速度的變化率,就像加速度是速度變化率一樣。
物體鏇轉點上的平移加速度由下式給出,
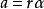 角位移
角位移其中r是與鏇轉軸線的半徑或距離。 這也是加速度的切向分量:它與點的運動方向相切。 如果該分量為0,則運動是均勻的圓周運動,速度僅在方向上改變。
徑向加速度(垂直於運動方向)由下式給出,
 角位移
角位移它指向鏇轉運動的中心,並且通常被稱為向心加速度。
 角位移
角位移角加速度是由扭矩引起的,根據正和負角頻率的慣例,它可以具有正值或負值。 扭矩和角加速度的比率(啟動,停止或以其他方式改變鏇轉的困難程度)由慣性矩給出:T=I 。
運動學方程
 角位移
角位移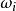 角位移
角位移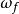 角位移
角位移 角位移
角位移當角加速度恆定時,五個角位移 ,初始角速度 ,最終角速度 ,角加速度 和時間t可以通過運動學的四個方程相關聯:
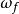 角位移
角位移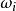 角位移
角位移 角位移
角位移= + t
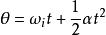 角位移
角位移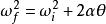 角位移
角位移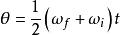 角位移
角位移矢量表達式
上述發展是一般鏇轉運動的特殊情況。在一般情況下,角位移,角速度,角加速度和扭矩被認為是向量。
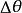 角位移
角位移角位移被認為是沿著軸指向的幅度等於 的矢量。使用右手規則來確定其沿軸的方向,如果右手的手指捲曲以指示對象鏇轉的方式,則右手的拇指指向向量的方向。
角速度矢量也以與其所產生的角位移相同的方式沿著鏇轉軸指向。如果磁碟從上方逆時針鏇轉,其角速度矢量向上指向。類似地,如果角加速度長時間保持,則角加速度矢量沿著與角速度將指向的相同方向沿鏇轉軸指向。
扭矩矢量沿著扭矩傾向於引起鏇轉的軸線點。為了保持圍繞固定軸的鏇轉,總扭矩矢量必須沿著軸線,使得其僅改變角速度矢量的大小而不是方向。在鉸鏈的情況下,只有沿著軸的轉矩矢量的分量對鏇轉產生影響,其他力和轉矩由結構補償。
示例與套用
恆定角速度
圍繞固定軸鏇轉的最簡單的情況是恆定的角速度。 然後總轉矩為零。對於圍繞其軸鏇轉的地球的例子,摩擦力很小。 對於風扇,電機施加扭矩來補償摩擦。 類似於風扇,大規模生產製造業中發現的設備有效地顯示圍繞固定軸線的鏇轉。 例如,使用多軸車床將材料鏇轉在其軸上以有效地增加切割,變形和轉動的產生。鏇轉角度是時間的線性函式,模360°是周期函式。其中一個實例就是圓軌道的兩體問題。
向心力
內部拉伸應力提供將紡絲物體保持在一起的向心力。剛體模型忽略了伴隨的應變。如果身體不僵硬,這種應變將導致其變形。這表示為由於“離心力”引起的對象改變形狀。
彼此鏇轉的天體通常具有橢圓軌道。圓周軌道的特殊情況是圍繞固定軸線的鏇轉的示例:該軸線是通過垂直於運動平面的質心的線,向心力由重力提供,另見天體問題。這通常也適用於鏇轉天體,因此除了角速度相對於其密度而言,角速度太高,所以不需要固體保持在一起。 例如,鏇轉天體的水必須至少需要3小時18分鐘才能鏇轉,不管大小如何,或者水將分離。如果流體的密度較高,則時間可以較少。