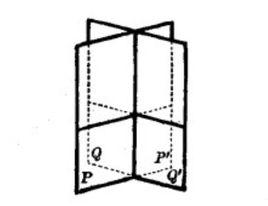
基本介紹
定義1 延長二面角的兩個半平面,與原二面角的平面角不相鄰的二面角稱為原二面角的對頂二面角,與原二面角的平面角相鄰的二面角稱為原二面角的 補二面角。
從定義知,二面角及其對頂二面角是其任一補二面角的補二面角 。
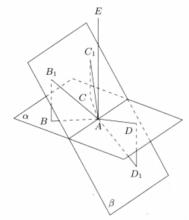 圖1
圖1相關定理
定理1 二面角的平面角與其對頂二面角的平面角相等,與其補二面角的平面角互補 。
定義2 把二面角的平面角二等分的半平面稱為該二面角的內平分平面;把二面角其中-個補二面角的平面角二等分的半平面稱為該二面角的外平分平面.
從定義2知,二面角的外平分平面是其對應補二面角的內平分平面。
定理2 二面角的內平分平面和其對應補二面角的外平分平面是唯一的。
證明 假設二面角的平面角是2α,二面角的內平分平面不是唯一的,還存在另一內平分平面,兩內平分平面的二面角的平面角是β>α,因而其中一個內平分平面與二面角一半平面所得的二面角的平面角是α+β> 2α,與內平分平面的定義矛盾,所以二面角的內平分平面是唯一的。同理可證二面角其對應補二面角的外平分平面是唯一的。
我們容易得到
定理3 二面角的內平分平面與外平分平面互相垂直,二面角的內平分平面與其對頂二面角的內平分平面共面,兩個外平分平面共面。
定理4 一個半平面是二面角的內平分平面的充要條件是該半平面上任意一點到二面角的兩個面的距離相等。
證明 充分性
如圖2,設A是平面γ內的一點,AB⊥α,AC⊥β,垂足分別是B和C,AB= AC,如果點A在二面角α-a-β的棱a上,則結論成立,如果點A不在a上,作BD⊥a,與a相交於點D,連AD、CD。由前面的證明知道∠BDC是二面角α-a-B的平面角。又因為△ABD≌△ACD,所以∠ADB= ∠ADC,因此平而γ是二面角α-a-β的內平分平面。
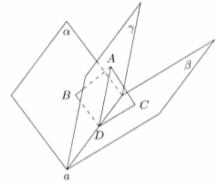 圖2
圖2必要性
在二面角α-a-β的內平分平面γ內取-點A,,如果點A在a上,那麼結論成立。如果點A不在a上,作AB⊥α,AC⊥β,垂足分別是B和C,做BD⊥a,與a相交於點D,連AD、CD。因為AB⊥α,AC⊥β。所以AB⊥a,AC⊥a,即a⊥平面ABC。又因為BD⊥a,所以a⊥平面ABD,由於過點A且與a垂直的平面只有一個,所以A、B、C、D共面,於是得CD⊥a,所以∠BDC是二面角α-a-β的平面角,因此∠ADB=∠ADC,於是△ABD≌△ACD,所以AB= AC 。