提出者
加斯帕爾·蒙日(Gaspard Monge,1746~1818),法國數學家、化學家和物理學家。
定理內容及證明
內容
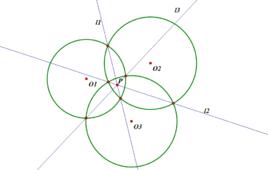
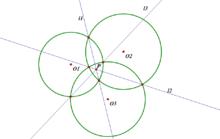
平面上任意三個不同心圓,若這三個圓圓心不共線,則三條根軸相交於一點,這個點叫它們的根心;若三圓圓心共線,則三條根軸互相平行。
引理
 蒙日定理
蒙日定理 蒙日定理
蒙日定理 蒙日定理
蒙日定理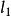 蒙日定理
蒙日定理 蒙日定理
蒙日定理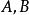 蒙日定理
蒙日定理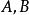 蒙日定理
蒙日定理 蒙日定理
蒙日定理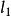 蒙日定理
蒙日定理 蒙日定理
蒙日定理 蒙日定理
蒙日定理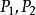 蒙日定理
蒙日定理對於平面上的一個圓⊙和不在圓上的任一點,過做一條直線交 ⊙於兩點(若直線與圓相切則設兩點重合),由圓冪定理可知為定值(即與的位置無關),我們把這個定值記作Ω(P),叫做P對⊙的冪。明顯的,Ω(P)隨著P點位置的變化而變化,且對於兩個到點距離相同的兩點,Ω(P)=Ω(P)。
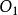 蒙日定理
蒙日定理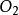 蒙日定理
蒙日定理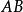 蒙日定理
蒙日定理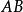 蒙日定理
蒙日定理 蒙日定理
蒙日定理 蒙日定理
蒙日定理對於平面上兩個相交的圓 ⊙, ⊙,設它們的公共弦為,在直線上任取一點,注意到Ω(X)==Ω(X),我們把這條弦成為兩圓的“等冪線”,也叫做“根軸”。明顯的,兩圓等冪線上的點對兩圓的冪相等。對於平面上兩個內切的圓,根軸為它們的公切線,對於兩個外切的圓,根軸為它們的內公切線。
對於平面上兩個外離的圓,使用勾股定理與圓冪定理易證根軸與兩圓的連心線相垂直。
證明
 蒙日定理
蒙日定理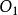 蒙日定理
蒙日定理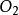 蒙日定理
蒙日定理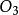 蒙日定理
蒙日定理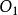 蒙日定理
蒙日定理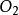 蒙日定理
蒙日定理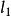 蒙日定理
蒙日定理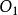 蒙日定理
蒙日定理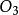 蒙日定理
蒙日定理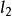 蒙日定理
蒙日定理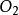 蒙日定理
蒙日定理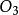 蒙日定理
蒙日定理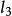 蒙日定理
蒙日定理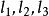 蒙日定理
蒙日定理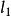 蒙日定理
蒙日定理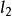 蒙日定理
蒙日定理 蒙日定理
蒙日定理設平面上有⊙ ,⊙ ,⊙ 三個圓,⊙ 與⊙ 的根軸為 ,⊙ 與⊙ 的根軸為 ,⊙ 與⊙ 的根軸為 。即證 共點。考察 與 的交點
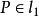 蒙日定理
蒙日定理 蒙日定理
蒙日定理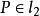 蒙日定理
蒙日定理 蒙日定理
蒙日定理 蒙日定理
蒙日定理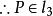 蒙日定理
蒙日定理 蒙日定理
蒙日定理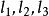 蒙日定理
蒙日定理∵Ω(P) =Ω(P) ∵Ω(P) =Ω(P)Ω(P) =Ω(P) 共點。得證。
套用
 蒙日定理
蒙日定理在此僅給出一道套用到此定理的例題。