ADP是最優控制領域新興起的一種近似最優方法,是當前國際最最佳化領域的研究熱點。在人工智慧領域,強化學習、人工神經網路、模糊系統、演化計算等方法的發展和豐富,提出了很多求解非線性系統最佳化問題的解決思路和具體技術方法。而ADP以傳統的最優控制為理論基礎,融合人工智慧的先進方法,提出了解決大規模複雜非線性系統最佳化控制問題的解決方法。
20世紀50年代,美國學者貝爾曼(R.E.Bellman)為解決非線性動態系統多級決策的控制問題,提出了動態規劃方法,並於1957年出版了《動態規劃》一書。動態規劃,從本質上講是一種非線性規劃方法,其核心是貝爾曼最優性原理。這個原理可以歸結為一個基本遞推公式,從而使決策過程連續遞推,並將一個多步(級)決策問題化簡為多個一步(級)決策問題,從末端開始到始端逆向遞推,從而簡化了求解過程。動態規劃由於眾所周知的弱點是其計算量和存儲量會隨著狀態和控制的維數的增加而急劇增長,這就是所謂的“維數災”(Curse of Dimensionality)問題,再加上在實際套用中通常無法得到精確的數學解析表達式,故其套用範圍受到了很大限制。
1977年,美國學者Paul J. Werbos首次提出了自適應動態規劃(ADP)。ADP是一種新的非線性最佳化方法,該方法融合了強化學習(Reinforcement Learning,RL)和動態規劃(Dynamic Programming,DP)的思想,模擬人通過環境反饋進行學習的思路,被認為是一種非常接近人腦智慧型的方法。該方法有效地解決了動態規劃“維數災”的難題。因此,ADP是一種適合於解決複雜非線性系統最佳化控制的新方法。
1997年,Prokhorov 和Wunsch討論了HDP, DHP和全局雙重啟發式動態規劃(GDHP)的設計,並提出了ADP的實現方法與訓練步驟。
ADP是利用函式近似結構來逼近動態規劃方程中的性能指標函式和控制策略,使之滿足貝爾曼最優性原理,進而獲得最優控制和最優性能指標函式。
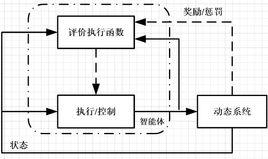
ADP一般包括三個部分:動態系統(dynamic system)、評價執行函式(critic performance index function) 環節、執行/控制(action/control)環節,每個環節均可由神經網路來代替。其中動態系統(或稱為被控對象)對應於建立的模型,執行/控制環節用來近似最優控制策略,評價執行函式環節是基於Bellman最優性原理進行參數更新,評價網路和執行網路的組合成了一個智慧型體。執行/控制作用於動態系統, 評價執行函式由動態系統產生獎勵或是懲罰作用來影響。執行/控制環節輸出控制動作,評價執行函式的輸出是基於貝爾曼最優性原理的代價函式值,即以輸出代價函式值最小為目標調整執行/控制環節使其輸出動作近似最優。
近年來,ADP的理論發展日趨完善,從ADP的研究表明,它具有其他非線性控制方法所沒有的優勢,如在處理“維數災”方面,展現了良好的套用效果和前景。ADP對非線性系統的穩定性、收斂性、最優性等的處理具有重要的作用;同時,在工業生產中具有較好的套用價值和前景。因此,ADP具有較好的理論意義和實踐意義。