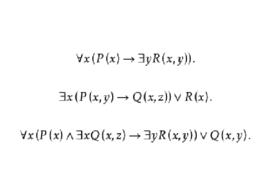基本介紹
定義
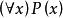 自由變元
自由變元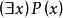 自由變元
自由變元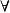 自由變元
自由變元 自由變元
自由變元在一個謂詞公式中,形如 或 的部分稱為x的約束部分。 、 後面所跟的x稱為量詞的指導變元或作用變元。P(x)稱為相應量詞的轄域或作用域。在作用域中x的一切出現,稱為約束出現,x稱為約束變元。若x的出現不是約束出現,則稱為自由出現,x稱為自由變元。
自由變元是不受約束的變元,雖然它有時也在量詞的作用域中出現,但它不受相應量詞中指導變元的約束。
注意點
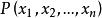 自由變元
自由變元對約束變元和自由變元有如下說明:自由變元是不受約束的變元,雖然它有時也在量詞的作用域內出現,但它不受相應量詞中指導變元的約束.故我們可把自由變元看做公式中的參數。若一個公式中的所有變元均呈約束出現而無自由出現,則此公式是確定的,能夠判別其真假。所以,呈約束出現的變元已經由不確定轉化為確定的了。從約束變元的概念可以看出, 是n元謂詞,它有n個相互獨立的自由變元,若對其中k個變元進行約束則成為n-k元謂詞,因此,謂詞公式中如果沒有自由變元出現,則該公式就成為一個命題。
主要題型
為了正確地理解謂詞公式,必須準確地判斷出量詞的作用域以及哪些是自由變元,哪些是約束變元。一般地,判斷量詞的作用域要看其後是否跟有括弧,若有括弧,則括弧內的子公式為相應量詞的作用域,否則與量詞鄰接的子公式為其作用域。判斷給定公式中的個體變元是約束變元還是自由變元,關鍵看它是自由出現還是約束出現。
例題說明
例1 指出下列公式的指導變元、作用域、約束變元和自由變元。
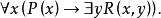 自由變元
自由變元(1)
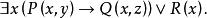 自由變元
自由變元(2)
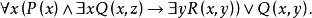 自由變元
自由變元(3)
解:
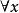 自由變元
自由變元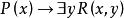 自由變元
自由變元 自由變元
自由變元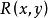 自由變元
自由變元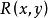 自由變元
自由變元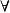 自由變元
自由變元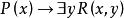 自由變元
自由變元(1) x是指導變元, 的作用域為 ;y也是指導變元, 的作用域為 。在該作用域 中,x是自由出現,y是約束出現。在 的作用域 中,x、y都是約束出現。
 自由變元
自由變元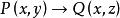 自由變元
自由變元(2) x是指導變元,相應量詞 的作用域為 ,從左向右算起,變數x的第一、二次出現是約束出現,x的第三次出現是自由出現。變數y、z的出現都是自由出現。
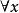 自由變元
自由變元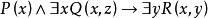 自由變元
自由變元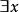 自由變元
自由變元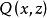 自由變元
自由變元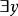 自由變元
自由變元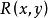 自由變元
自由變元(3) x、y是指導變元, 的作用域是 , 的作用域是 , 的作用域是 。x的最後一次出現為自由出現,其餘為約束出現,y的第一次出現為約束出現,第二次出現為自由出現。變元z為自由出現。
受量詞約束的個體變元稱為自由變元。
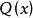 自由變元
自由變元例2 “x是整數”可以表示為 。它是一個命題函式,而不是命題,不能判斷真假。故x是自由變元。
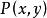 自由變元
自由變元例3 “x<y”可表示為“ ”。它也是一個命題函式,而不是命題。故x和y都是自由變元。