簡介
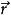 自旋算符
自旋算符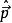 自旋算符
自旋算符自旋角動量是電子的內稟屬性,無經典對應,即不能象角動量一樣寫成 和 的函式,而是描述電子狀態的又一個新的力學量。象其它力學量一樣,自旋角動量也用一個算符表示。
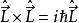 自旋算符
自旋算符利用角動量的定義: ;
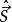 自旋算符
自旋算符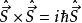 自旋算符
自旋算符引入 : 。跟經典角動量的共性就是它們各自的對易關係一致。
自旋算符的對易關係
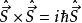 自旋算符
自旋算符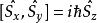 自旋算符
自旋算符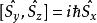 自旋算符
自旋算符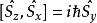 自旋算符
自旋算符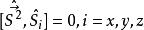 自旋算符
自旋算符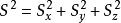 自旋算符
自旋算符角動量平方算符:
自旋算符的本徵值
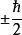 自旋算符
自旋算符由於在空間任何方向上的投影只能取兩個數值,所以三個算符的本徵值都是兩個 ,它們的平方就都是 :
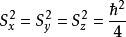 自旋算符
自旋算符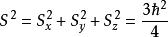 自旋算符
自旋算符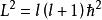 自旋算符
自旋算符類似 ;
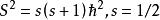 自旋算符
自旋算符令
s與l相當,稱s為自旋量子數。(l 叫軌道量子數或角量子數)。
自旋算符的本徵波函式
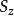 自旋算符
自旋算符本徵:當我們僅研究自旋性質時,系統的空間部分波函式可以視為常數,選擇 表象,則算符的兩個本徵態為:
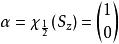 自旋算符
自旋算符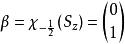 自旋算符
自旋算符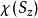 自旋算符
自旋算符一般態:當體系自旋處在一般態 時,由前面基本假設,為自旋算符本徵函式的線性組合,記為:
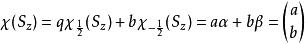 自旋算符
自旋算符這樣的列矩陣形式稱為旋量,2行1列的矩陣二分量旋量,實際上也是二維Hilbert Space的一個矢量。
自旋算符的么正變換
兩種表象中的電子自旋算符的矩陣表示可以由兩種表象之間的變換矩陣作么正變換相互轉換。根據《量子力學》教科書中的有關論述,算符F 的態矢和矩陣表示從A表象到B表象的變換式分別為
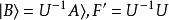 自旋算符
自旋算符上式等價於:
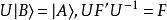 自旋算符
自旋算符式中| B〉和F′為算符F 在B表象中的態矢和矩陣表示,| A〉和F為F 在A表象中的態矢和矩陣表示,U為從A表象到B表象的變換矩陣。雖然二者等價,但我們認為,為了使計算方便,選用第二個式子為表象之間的變換式更好。
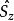 自旋算符
自旋算符以從Sx表象到Sz表象的變換為例,設由Sx表象變換到Sz表象的變換矩陣為
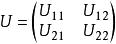 自旋算符
自旋算符U必須為么正矩陣,即滿足
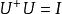 自旋算符
自旋算符可以計算得到由Sx表象到Sz表象的變換矩陣為
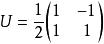 自旋算符
自旋算符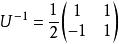 自旋算符
自旋算符對電子自旋在Sx表象的表示作么正變換即可得到它們在Sz表象的表示,即對Sy表象的變換也可以作類似的討論。
