定理及證明
 聚點原理
聚點原理定理有界無窮點集至少有一個聚點(極限點) 。
此定理叫做 聚點原理。
 聚點原理
聚點原理 聚點原理
聚點原理 聚點原理
聚點原理 聚點原理
聚點原理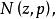 聚點原理
聚點原理 聚點原理
聚點原理 聚點原理
聚點原理 聚點原理
聚點原理 聚點原理
聚點原理 聚點原理
聚點原理 聚點原理
聚點原理 聚點原理
聚點原理證明: 將包含在中心位於原點,各邊平行於坐標軸的正方形內,若沒有聚點,則對於中每一點z,存在這樣一個鄰域使得在這個鄰域內只含的有限個點,且這些鄰域的全體將復蓋住,由 有限復蓋定理,在這些鄰域中只要有限個鄰域就將復蓋住(當然是有界閉集)。這樣一來,點集也只有有限個點屬於,這與為無窮點集而又完全包含在k內相矛盾。從而定理成立 。
聚點的定義
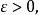 聚點原理
聚點原理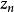 聚點原理
聚點原理任給存在無窮多個滿足
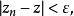 聚點原理
聚點原理 聚點原理
聚點原理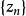 聚點原理
聚點原理則稱為複數序列的一個聚點。
有的序列可以有多個聚點。例如,實數序列
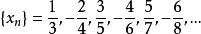 聚點原理
聚點原理就有兩個聚點1和-1.當序列的極限存在時,序列的極限是此序列的唯一聚點。
推論及證明
推論
在擴充複平面上每一個無窮點集至少有一個聚點(有限點或無窮遠點) 。
推論證明
 聚點原理
聚點原理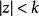 聚點原理
聚點原理 聚點原理
聚點原理 聚點原理
聚點原理根據假設,對於E來說,只有兩種可能,或者存在某一個圓域:它含有E的無窮多個點,因而含有E的聚點(由聚點原理得知) ,或者在每一個圓域內只有E的有限個點,此時在無窮遠點的任意鄰域:內有E的無窮多個點,因此,點是E的聚點,從而推論得證。
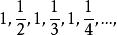 聚點原理
聚點原理規定在一個數列中如有某數重複出現無窮多次,則該數也看作數列的聚點,例如數列中0 是一個聚點,由於1在數列中出現無窮多次,故1也是聚點。按照這個規定,顯然任何有界無窮數列必至少有一個聚點 。
有限復蓋定理
閉集
先介紹閉集的概念。
如果點集E包含它的所有聚點在內,則稱E為 閉集。
定理介紹
 聚點原理
聚點原理海恩-波萊爾定理(Heine-Borel)假設E為有界閉集,且對E內每一點z都作一個以這一點為圓心的圓域(這個圓的半徑沒有限制,它可以取任意正實數),則在這些圓中必可以找到有限多個來把有界閉集E復蓋住,換句話說,E的每一點至少屬於這有限個圓域中的一個圓域的內部。此定理又叫做 有限復蓋定理,它是複變函數論里的重要定理。
下面套用數學分析中的矩形套定理來證明有限復蓋定理。
證明: 如果E是有限集,定理顯然成立。
設E是無限集,則我們用反證法來證明,設Q為一個各邊平行於坐標軸,以坐標原點為中心的正方形,並且將E包含在內,若定理不成立,則將Q分成四個全等的正方形時,在這四個正方形上的E的四個子集中至少有一個不能用上述有限個圓心屬於E的圓域所復蓋,我們把這個子集所在的正方形記為Q,並且再把它用同樣方式分成四個全等的正方形,同樣,我們又得到一個正方形Q,繼續這種分法,我們得到Q,它包含E的一部分,而且對這一部分來說,我們的定理是不成立的,也就是說,E的這一部分必須用無窮多個圓K才能復蓋住,但因這些正方形組成了一個閉正方形套(特殊的矩形域套) :
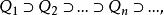 聚點原理
聚點原理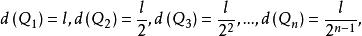 聚點原理
聚點原理並且它們的對角線的長分別為
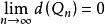 聚點原理
聚點原理因此,。
 聚點原理
聚點原理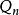 聚點原理
聚點原理 聚點原理
聚點原理 聚點原理
聚點原理 聚點原理
聚點原理 聚點原理
聚點原理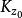 聚點原理
聚點原理 聚點原理
聚點原理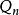 聚點原理
聚點原理 聚點原理
聚點原理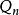 聚點原理
聚點原理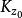 聚點原理
聚點原理 聚點原理
聚點原理根據閉矩形套定理,存在唯一一點屬於所有這些正方形,於是當n充分大時,在的任一個鄰域必須包含正方形Q,因而也就包含著E的點,並且是無窮多個點,不然的話,E的這個子集能夠被有限個圓所復蓋住,但這是不可能的。所以為E的聚點,因為E為閉集,所以屬於E,設圓的半徑為,選這樣大的一個n,使得正方形的對角線的長小於,於是我們得到所有屬於的E的點都被圓所復蓋住,但是根據我們最初的假設,必須有無窮個圓才能把它們復蓋住,這是個矛盾,從而定理得證 。
有限復蓋定理的逆定理也成立。

