概述
按照圖形理論,聚集係數是表示一個圖形中節點聚集程度的係數,證據顯示,在現實中的網路中,尤其是在特定的網路中,由於相對高密度連線點的關係,節點總是趨向於建立一組嚴密的組織關係。在現實世界的網路,這種可能性往往比兩個節點之間隨機設立了一個連線的平均機率更大。
在很多網路中,如果節點v1連線於節點v2,節點v2連線於節點v3,那么節點v3很可能與v1相連線。這種現象體現了部分節點間存在的密集連線性質。可以用聚類係數(CC)來表示,在無向網路中,聚類係數定義為:
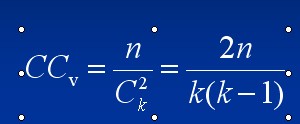
全局集聚係數
全局集聚係數全局集聚係數是基於結點三元組的。一個三元組是其中有兩條(開三元組)或三條(閉三元組)無向邊連線的三個結點。一個三角由三個封閉的三元組構成,(三元組)集中在每一個結點上。全局集聚係數是所有三元組(包括開和閉的)中封閉三元組的數目。

局部集聚係數
圖中一個結點的局部集聚係數表示了它的相鄰結點形成一個團(完全圖)的緊密程度。Duncan J. Watts和Steven Strogatz在1998年引入了度量一個圖是否是小世界網路的方法。
定義
G = (V, E) : 圖G包含一系列結點V和連線它們的邊E.
eij : 連線結點i與結點j的邊.
Ni = {vj : eij∈E ∩ eji∈E} : 節點vi的所有相鄰結點集合.(包括兩種不同的連線方向)
ki= |{Ni}|: vi相鄰結點的數量.
結點vi的局部集聚係數Ci是它的相鄰結點之間的連線數與它們所有可能存在連線的數量的比值。對於一個有向圖,eij 與 eji是不同的,因而對於每個鄰結點 Ni在鄰結點之間可能存在有 ki(ki − 1)條邊(ki 是結點的出入度之和)。
網路的平均集聚係數
整個網路的集聚係數由Watts和Strogatz定義為所有結點n的局部集聚係數的均值:
如果一個圖的平均集聚係數顯著高於相同結點集生成的隨機圖,而且平均最短距離與相應隨機生成的隨機圖相近,那么這個圖被認為是小世界的。
有更高平均集聚係數的網路被發現有著模組結構,同時在不同結點中還有更小的平均距離。
