什麼是模糊聚類法
在經濟學、社會學、生物學、氣象學、醫藥等許多領域的研究中,經常遇到處理具有模糊性的數據問題。這裡所謂的模糊性,主要是指客觀事物差異的中間過渡中的“不分明性”和“邊界不清”的意思,例如商品評價中“質量好、比較好、比較差等”,氣象災害對農業產量的影響程度為“嚴重、重、輕”,病人患某種疾病的症狀是“重、輕”以及“有礦與無礦”,“冷、暖”“多雲間晴”都難以明確地劃清界限。
為了研究這方面的問題,1965年由美國自動控制專家查德(L.A.Zadeh)首先提出模糊集合的概念,之後成功的用數學方法描述模糊概念,從而產生了模糊數學。從模糊數學的誕生到現在也僅有幾十年的歷史,其理論尚不十分完善,但是這門科學的發展非常迅速,模糊數學套用的觸角已伸人到國民經濟領域的各個學科。模糊數學的理論基礎是模糊集理論,下面介紹模糊集理論套用到聚類分析中從而產生了模糊聚類法 。
模糊聚類的基本概念
特徵函式
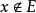 模糊聚類法
模糊聚類法對於一個普通的集合E,空間中任一元素x要么有x∈E,要么有 ,二者必居其一,這一特徵用·個函式表示為
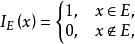 模糊聚類法
模糊聚類法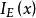 模糊聚類法
模糊聚類法稱k(z)為集合E的 特徵函式 。
例如,設E為某地區在某年度完成國家利稅的企業全體,這時對該地區任一企業x,我們可用特徵函式描述它是否完成了國家利稅,即
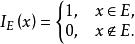 模糊聚類法
模糊聚類法隸屬函式與模糊集
如果我們進一步描述某企業完成國家利稅的程度大小時,僅用特徵函式就不夠了。模糊集理論變將特徵函式的概念推廣到[0,1]內取值的函式以度量這種程度的大小,這個函式稱為集合E的 隸屬函式,記為E(x),即對於每一個元素x,有[0,1]內的一個數E(x)與之對應 。
若在集合E上定義了一個隸屬函式,則稱E為 模糊集。
模糊矩陣及其褶積
 模糊聚類法
模糊聚類法 模糊聚類法
模糊聚類法(1)若矩陣 A的各元素 滿足0≤ ≤1,則稱 A為模糊矩陣 。
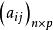 模糊聚類法
模糊聚類法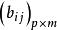 模糊聚類法
模糊聚類法(2)設 A= 和 B= 為兩個模糊矩陣,令
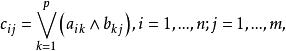 模糊聚類法
模糊聚類法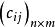 模糊聚類法
模糊聚類法則稱矩陣 C= 為模糊矩陣 A與 B的褶積,記為 C= AB。
其中“∨”和“∧”的含義為:a ∨b=max{a,b}, a ∧ b=min{a,b}。
顯然,兩個模糊矩陣的褶積仍為模糊矩陣。
模糊等價矩陣及其λ截陣
設方陣 A為一模糊矩陣,若 A滿足
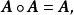 模糊聚類法
模糊聚類法則稱 A為 模糊等價矩陣。
模糊等價矩陣可以反映模糊分類關係的傳遞性,即描述諸如“甲像乙,乙像丙,則甲像丙”這樣的關係。
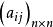 模糊聚類法
模糊聚類法設 A=為一個模糊等價矩陣,0≤λ≤1為一個給定的數,令
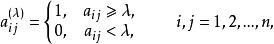 模糊聚類法
模糊聚類法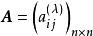 模糊聚類法
模糊聚類法則稱矩陣為 A的 λ-截陣 。
模糊聚類方法
具體步驟如下:
(1)計算相似係數矩陣R或樣品的距離矩陣D 。
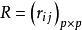 模糊聚類法
模糊聚類法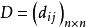 模糊聚類法
模糊聚類法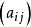 模糊聚類法
模糊聚類法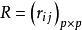 模糊聚類法
模糊聚類法(2)將(或中的元素縮到0與1之間形成模糊矩陣,我們統一記為 A=,例如對相似係數矩陣,可令
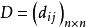 模糊聚類法
模糊聚類法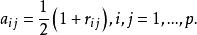 模糊聚類法
模糊聚類法對於距離矩陣,可令
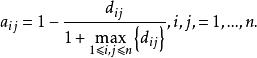 模糊聚類法
模糊聚類法(3)建立模糊等價矩陣
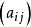 模糊聚類法
模糊聚類法一般說來,上述模糊矩陣 A=不具有等價性,這可以通過模糊矩陣的褶積將其轉化為模糊等價矩陣,具體方法如下:
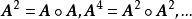 模糊聚類法
模糊聚類法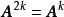 模糊聚類法
模糊聚類法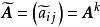 模糊聚類法
模糊聚類法計算,直到滿足,這時模糊矩陣 A 便是一個模糊等價矩陣。記。
(4)聚類
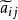 模糊聚類法
模糊聚類法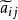 模糊聚類法
模糊聚類法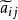 模糊聚類法
模糊聚類法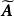 模糊聚類法
模糊聚類法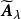 模糊聚類法
模糊聚類法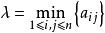 模糊聚類法
模糊聚類法將按由大到小的順序排列,從λ=1開始,沿著由大到小的次序依次取λ=,求的相應的λ-截陣,其中元素為1的表示將其對應的兩個變數(或樣品)歸為一類,隨著λ的變小,其合併的類越來越多,最終當A=min{a。)時,將全部變數(或樣品)歸為一類。

