基本介紹
群內相關整群抽樣的方差與群內次級或基本單元之間的差異或同質性(相似程度)有關，為此引進群內相關係數這個概念。群內相關係數(interclass correlation coefficient) 表示同一群內不同次級或基本單元的變數值對總體均值的離差乘積的期望值與總體中所有次級或基本單元變數值對總體均值離差平方的期望值之比，即
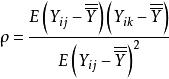群內相關
群內相關
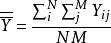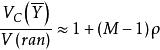群內相關
群內相關其中N為總體中包括的群，M為每群中包括的總體單位數， Y為第i個群內第j個個體的觀測值， 。整群抽樣與簡單隨機抽樣之間的方差存在如下關係： ， 即為基什的deff(設計效果)。從理論上，若ρ>0，在樣本總含量已給定的情況下，與簡單隨機抽樣比採用整群抽樣所得結果的精確度要低。若ρ<0，則採用整群抽樣所得結果的精確度要高。若ρ=0，則兩者精度幾乎是等價的 。
當N很大時，
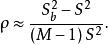群內相關
群內相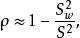關
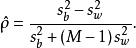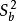群內相關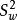
群內相關
群內相關其中：總體群間方差 (大致等於總體方差S 與總體群內方差 之差)（證明見參考資料） 。
群內相關係數的取值
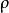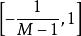群內相關
群內相關的取值範圍為 ，它可分為以下幾種情況 ：
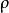| 群內相關 | 群內小單元的取值 |
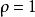 群內相關 | 沒有差異 |
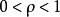 群內相關 | 差異較小 |
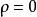 群內相關 | 隨機 |
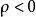 群內相關 | 差異較大 |
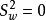群內相關 群內相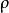關
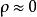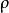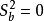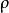群內相關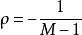 群內相關
群內相關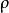 群內相關
群內相關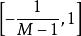 群內相關 群內相關如果群內次級或基本單元變數值都相等，則 ，此時 取最大值1；如果群內方差與總體方差相等，則 ，此時表示分群是完全隨機的；如果群內方差大於總體方差時，則 取負值；如果 時， 達到極小值，此時 。因此 取值範圍是 。
可以證明
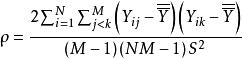群內相關
群內相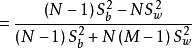關
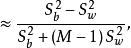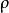群內相關 群內相關根據樣本，可以用下式估計 ：
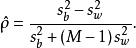群內相關整群抽樣的設計效應為
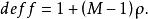群內相關
群內相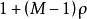關
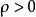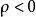群內相關 群內相關由此可見，按相同的樣本量(以次級單元的個數計)，整群抽樣的方差約為簡單隨機抽樣的方差的 倍。當 時，deff>1，整群抽樣的精度比簡單隨機抽樣低；當 時，deff<1，整群抽樣的精度比簡單隨機抽樣高 。
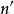群內相關設整群抽樣的樣本量(次級單元個數)為n，簡單隨機抽樣的樣本量為 ，則有
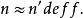群內相關