定義
矢量空間
實值函式ƒ定義在區間[ a, b]⊂' R的總變差是一維參數曲線 x→ƒ( x) , x∈[ a, b]的弧長。連續可微函式的總變差,可由如下的積分給出
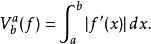 總變差
總變差任意實值或虛值函式ƒ定義在區間[ a, b]上的總變差,由
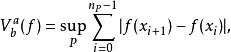 總變差
總變差定義。其中為區間[ a, b]中的所有分劃。
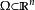 總變差
總變差定義在有界區域上的實值可積函式 ƒ的 總變差定義為
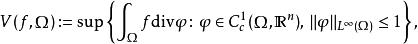 總變差
總變差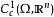 總變差
總變差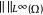 總變差
總變差其中 是Ω中的緊支集上全體連續可微向量函式構成的集合, 是本質上確界範數。
若ƒ可微,上式可簡化為
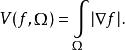 總變差
總變差度量空間
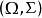 總變差
總變差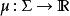 總變差
總變差在一個度量空間上,集函式,其總變差為:
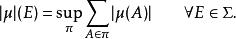 總變差
總變差 總變差
總變差 總變差
總變差其中為 E的劃分。 如果是符號測度,通過漢分解定理可知:
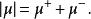 總變差
總變差可微定義證明
首先需要利用高斯散度定理證明一個等式。
引理
在假設條件下,下面的等式成立:
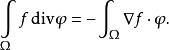 總變差
總變差引理證明
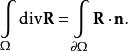 總變差
總變差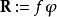 總變差
總變差由高斯散度定理,將代入,可得
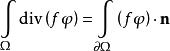 總變差
總變差 總變差
總變差 總變差
總變差由於在的邊界上,從而
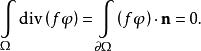 總變差
總變差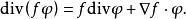 總變差
總變差注意到代入上式,移項即得
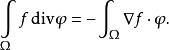 總變差
總變差如果函式 f的總變差有限,則稱函式 f為有界變差函式。
參閱
•有界變差
•總變差規則化
•二次變差

