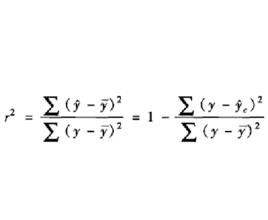總變異的分割
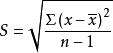可決係數
可決係數一個特定數值對於其平均值的偏離，稱為 離差，而一變數的各數值對於其平均值的偏離，稱為 變異。通常用 離差平方和來描述變異程度。離差平方和又簡稱平方和(Sum of square)。在研究單變數的離中趨勢描述時，我們已經接觸了離差平方和的概念，樣本標準差的定義公式中就直接使用了上述概念。平方和被相應的自由度去除，得到 平均平方，簡稱為 均方(Mean square)。樣本標準差就是被自由度(n-1)所平均的x對於離差均方的算術平方根。下面我們將套用平方的概念去開發測度一個回歸方程擬合協變關係效果的量數。
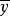可決係數
可決係數
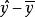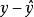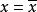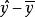可決係數
可決係數 可決係數 可決係數先結合圖1分析一下在因變數y倚自變數x回歸前提下y值的離差。y值對其平均數的離差可以看作是由兩部分合成的，一是y的回歸擬合值對平均數的離差()，另一是y值對於擬合值的離差()。前者呈線性變化，在時，=0，x取值越偏離，這一離差就越大，存在著這樣的函式關係：
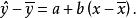可決係數
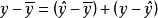可決係數這一離差完全是由y倚x的回歸關係決定的，因而稱為 已解釋離差(Explained deviation)。後者呈隨機變化，與y倚x的回歸關係無關，因而稱為 未解釋離差(Unexplained deviation)。總離差與已解釋離差、未解釋離差的關係寫成公式是：。
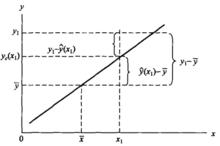圖1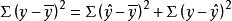
可決係數
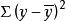可決係數總離差的平方和，簡稱 總平方和，用SST表示，又稱作 總變差(Total variation)。已解釋離差的平方和，簡稱 回歸平方和，用SSR表示，又稱作 已解釋變差(Explained variation)。未解釋離差的平方和，簡稱 誤差平方和，用 SSE表示，又稱作 未解釋變差(Unexplained variation)。可以證明，由總離差的分解公式能推出總變差的分解公式：，或：SST=SSR+SSE。將上式兩邊都除以，得：已解釋變差/總變數 +未解釋變差/總變差=1，即
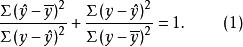可決係數這樣我們就把在絕對數意義上對總變差的分割，改換成在相對數意義上對總變差的分割，這對於研究回歸方程的擬合效果很有幫助 。
樣本可決係數
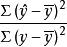可決係數
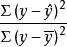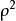可決係數
可決係數從公式(1)看到，若以總變差為基數，相對數表示的是回歸關係已經解釋的y值變異在其總變異中所占的比率，而相對數則表示回歸關係不能解釋的y值變異在總變異中所占的比率。前者正是我們要尋求的測度回歸方程擬合y對x的協變關係效果的量數，稱為 可決係數(Coefficient of determination)。產生於樣本數據的可決係數是樣本可決係數，用r 表示。在總體回歸分析中，相對於樣本可決係數的是總體可決係數，用表示。因此，樣本可決係數的定義公式是 ：
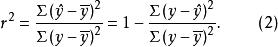可決係數相關係數與可決係數的關係
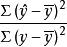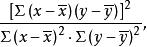可決係數
可決係數由可以推導到所以存在著這樣的關係：可決係數是相關係數的二次冪。因此，也可以在求得可決係數的基礎上計算相關係數，方法是將可決係數開平方，至於平方根的符號，則取與回歸方程斜率b相同的符號。正是因為存在這樣的關係，我們用r 作為可決係數的符號，而沒有另用別的字母。
即然r和r 兩者問存有這樣的聯繫，那么它們的描述分析作用是否相同呢?我們認為，儘管兩者對變數間協變關係的解釋有相通的一面，但是兩者間的區別也是不容忽視的。
首先，可決係數是在擬合回歸方程後進一步評價它的解釋作用，而回歸分析有其具體目的和假定前提。相關係數直接用於相關分析，它只描述變數間協變關係的密切程度，而不問哪個是自變數，哪個是因變數，相關分析也有3條假設前提：
(1) X和Y均為隨機變數。
(2) X和Y均服從常態分配，兩者不必相互獨立。
(3) 對於X所有取值，Y值的標準差都相等；對於Y所有取值，X值的標準差也都相等。
這樣看來，可決係數和相關係數所描述的問題性質不盡相同。
其次，可決係數取已解釋變差對總變差的比率形式，在運算上有直接的解釋意義。相關係數是沿交叉乘積和——協方差——相關係數的思想開發出來的，其最終公式形式不好作直接的解釋。儘管如此，在許多套用中，如果兩者都可以出現，我們還是更多地注意到r 值 。
總體可決係數
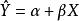可決係數總體可決係數是在總體中關於Y總變異中總體回歸方程已經解釋的變異所占比重的描述量數。它用下式表示
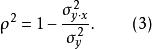可決係數 可決係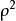數
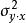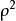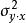可決係數
可決係數 可決係數 可決係數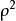 可決係數 可決係數在的定義公式中，是圍繞總體回歸直線的方差，是圍繞總體平均數的方差。作為總體參數，通常視為未知的，有待於用樣本統計量去估計。將和的無偏估計量分別代入上式，即得到估計量的公式
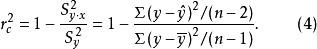可決係數不難發現，公式（2）與公式（4）略有不同，前者採用的是平方和比率的形式，而後者採用的是均方和比率的形式。
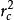可決係數稱為經調整樣本可決係數(Adjusted coefficient of determination)，它用於對總體可決係數進行點估計。經調整可決係數平抑了方程中自變數數目的對解釋作用的誇大，尤其在多元回歸分析中，因為對同一樣本k個自變數的回歸方程總比k-1個自變數的回歸方程求得已解釋變差小，經調整的可決係數在k個自變數的方程中已解釋變差除以(n-k-1)，而在(k-1)個自變數的方程中則除以(n-k-2) 。
