縮合聚合

縮合聚合

正文

具有兩個或兩個以上官能團的低分子化合物(單體)經多次重複地進行縮合反應，生成聚合物，並同時分出簡單的小分子（如水、醇、氨、鹵化氫等）的化學反應。當用雙官能團的單體時，形成線型聚合物；如果單體的官能度大於2，則可以得到支化或交聯的網狀聚合物。
歷史　早在1909年，美國L.H.貝克蘭就合成了酚醛樹脂，但縮合聚合成為兩大聚合反應類型之一，則是在1929年W.H.卡羅瑟斯系統地研究了雙官能化合物的縮合反應後。卡羅瑟斯等採用分子蒸餾方法除去酯化反應生成的水，製得高分子量的線型聚酯，其熔體可以紡成絲。後來相繼發現了能形成纖維的聚酯、聚醯胺等結晶性高分子，開創了以己二胺和己二酸為單體合成耐綸66纖維的工業。1940年英國J.R.溫菲爾德等人開發了主鏈含有苯環的聚酯（滌綸）樹脂。P.J.弗洛里研究了縮合聚合反應動力學，提出了縮聚過程中不同鏈長的高分子的官能團具有相等活性的理論，從而求得縮聚產物分子量的幾率分布，並針對多官能化合物的縮合聚合生成體型結構的交聯聚合物這一事實，引入了凝膠化理論。1958年P.W.摩根等發展了界面縮聚和後來的低溫溶液縮聚方法，為在高溫下不熔或能分解的雜環或芳環高分子的合成開闢了途徑。1961年C.S.馬維爾從多官能化合物單體的環化縮聚合成了聚苯並咪唑等一系列耐熱高分子。70年代以來，縮聚反應的研究趨向於合成各種功能高分子材料，並逐漸接近於天然高分子及生物高分子的合成。
縮聚反應的基本特徵　與烯類聚合不同，縮合聚合由於是單體官能團間的相互作用，通常只需要熱能就能開始進行聚合反應，而且除了產生熱分解、交聯等副反應以外，本質上沒有終止反應。
聚合物分子量隨時間逐步增加　在縮聚反應中，鏈增長是以緩慢和逐步反應的形式進行的。在反應體系內，沒有特定的反應活性中心，任何兩個分子都可以相互反應。在開始時形成二聚體，它再與另一單體分子生成三聚體或與另一二聚體生成四聚體，以後單體和各級聚合體以及聚合體之間繼續反應，聚合產物的分子量隨反應時間逐漸增大，最後達到一定程度的平衡。在反應後期所得到的聚合物分子量大小不一，形成相當寬的分子量分布。
A和B兩種官能團反應縮合生成新鍵時，副產物水分子不斷從體系中排出,添加的酸催化劑濃度是一定的,兩種官能團初始濃度【A】0＝【B】0時,通過反應速率方程式的演算，得到生成聚合物的數均聚合度與反應時間 t的關係式為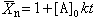：，即生成的聚合物的分子量隨反應時間而線性地增加。
不同鏈長的高分子具有相等活性　對於這種複雜的多步縮合反應體系，如果要對每一步反應進行解析是相當困難的。可以構想，隨著縮聚反應過程中分子鏈的增長，官能團的反應活性也將會有所變化。然而，從低分子化合物（如不同鏈長羧酸）的酯化反應研究結果表明，當羧酸的碳原子數大於 4時，其反應速率常數已趨於一定數值，不因鏈的加長而改變。因此在理論處理時可以假定官能團的反應活性與分子鏈長無關，即在縮聚過程中每一基元反應都以不變的反應速率進行。這樣就有可能選用任一平衡反應來代表整個縮聚平衡反應。
聚合度與反應程度關係密切　在縮聚反應中，可以用已參加反應的官能團所占的分數來表示其反應程度p。例如A─B型單體HO(CH2)nCOOH進行縮聚時，用實驗測定其羧基數目，最初為N0，縮聚反應進行到反應程度 p時羧基數為 N，則p＝(N0-N)/N0。此時生成的縮聚物的數均聚合度，反應程度與數均聚合度的關係為。具體的數值關係見表1 。縮聚高分子材料要具有必要的強度，其平均聚合度應在 100以上。這樣，反應程度必須達到99％以上。因此必須嚴格要求單體純度和反應條件。

縮合聚合

兩種組分要求等當量比　極少量的單官能雜質或一種雙官能單體的過量，對縮聚反應的最終分子量有顯著影響。當【A】0＜【B】0,即A─A、B─B型兩種單體不等摩爾時(例如B-B過量時)，最後聚合物末端均為過剩的官能團 B，縮聚反應就停止進行。也可以利用一種組分過量來調節控制聚合平衡時的平均分子量。設 A官能團完全起反應，B官能團過量的百分數為q，則聚合物的數均聚合度＝200/q（是以結構單元-A-A-或-B-B-為基準的聚合度,為以重複單元作基準的聚合度唒n的兩倍）。
如果在反應中添加少量單官能化合物（如R-B）作為分子量調節劑，則當NA＝NB，p接近於1時，最後的分子數為NRB,＝NA/NRB。可見,極少量的單官能雜質對最終分子量有顯著影響。反應時一種組分的揮發逸失或是由於副反應使得官能團分解或末端環化，均會限制生成的聚合物的分子量。
平均聚合度與小分子副產物的濃度成反比　很多重要的縮聚反應是化學平衡反應，縮聚反應的一個主要特點是伴隨著化學平衡。以等當量單體進行聚醯胺化為例，可用下列平衡來表示：

式中k1和k-1分別為正、逆反應速率常數,nw為反應體系中存在的水分子濃度（摩爾分數）。其平衡常數為：

由此可導出平均聚合度與反應平衡常數及水分子濃度的關係：

如果反應在密閉體系中進行,則nw＝p，即在確定的平衡常數下，縮聚產物的平均聚合度與小分子副產物的濃度成反比。而當水分子不斷從反應體系中除去，分子量增大，反應程度接近1時，則得到以下近似關係：

平衡常數愈大，對聚合物生成愈有利。平衡常數隨反應溫度、壓力而起變化，也由於單體的化學結構而有所變動。例如,在254℃生成耐綸66的聚醯胺化反應的平衡常數為300；在同樣溫度下,耐綸12為370,聚酯滌綸為0.73。可見，聚醯胺化反應的平衡常數大，容易生成高分子量的聚醯胺；而聚酯化的平衡常數很小，因此需要在高真空條件下完全排去反應所生成的低分子副產物，才能達到高分子量。
環鏈平衡　由於分子內官能團的相互反應，生成環狀結構產物因而存在環與鏈的平衡。例如 6－氨基己酸NH2(CH2)5COOH的縮合反應可以分兩個方向進行:分子內縮合形成環狀化合物己內醯胺和分子間縮聚生成線型高分子聚己醯胺，兩者是競爭反應，同時也構成了縮聚產物中環鏈間的平衡。表2列出ω-羥基酸與ω-胺基酸加熱縮合反應的產物，它隨亞甲基鏈長大小而各異。反應的方向主要決定於單體的分子結構（即成環的大小）、官能團間的距離和分子鏈的柔韌性。環鏈平衡通常與環的張力大小有關,5元環和6元環最穩定,一般不易生成線型高分子。如果升高溫度和降低反應物的濃度(即極度稀釋時)，都對環化反應有利。此外，縮聚物熱裂解時也有生成大環的機會。

縮合聚合

交換反應　在縮聚反應中，除了有小分子參與的可逆反應外，還存在著高分子鏈節間以及高分子末端未反應的官能團與鏈節間的交換反應，特別是在高溫或合適的催化劑作用下更易進行。在聚酯的生成反應中，酯基與醇或末端羥基很易起交換反應。這種交換反應的總酯鍵數與聚合物分子數目都沒有改變，所以不影響其數均分子量，但分子量分布則發生變化。例如，同樣長的兩個聚合物分子起交換反應會生成一長一短的分子鏈。又如，將平均分子量一高一低的兩種聚酯加熱熔融後，可以得到平均分子量在二者之間的聚合物，並且觀察到熔體粘度的下降。交換反應使各種大小分子量的分子重新進行分布，分子量大的分子數減小，所以重均分子量降低，對粘度有影響。長時間的交換反應最終會達到一個動態平衡的分子量分布。
縮聚產物的分子量分布　可以用實驗方法來測定，但按照P.J.弗洛里的理論，在任一階段不同鏈長高分子的官能團都有同等機會參與反應，因此可以用統計方法來推算不同反應程度時的分子量分布。
雙官能單體的線型縮聚反應　以A─B型聚酯為例，當縮聚反應進行至時間t時,官能團羧基（或羥基）的反應程度 p也可以作為已參與反應形成酯鍵的幾率。聚合度為X的X聚體需要連續構成X-1個酯鍵,則其幾率為pX-1，一個末端未反應和不成鍵的羧基（或羥基）出現的幾率為1-p。最初體系分子數為N0，縮聚反應進行t時間後分子數減少至N個，則X聚體分子的數目以NX表示時為：

NX＝NpX-1(1-p)＝N0pX-1(1-p)2

此式為線型縮聚反應產物分子量的數量分布函式，如果忽略端基的─H和─OH重量,則每一種分子的分子量就和聚合度X 成正比，X 聚體所占的重量分數為：

WX＝XNX/N0＝XpX-1(1-p)2

此式為分子量的重量分布函式。當反應程度p越大時,分子量分布也愈寬。
根據弗洛里分布函式，可以計算出數均聚合度和重均聚合度,由此可求得多分散係數（也稱最可幾分布）：

當反應程度p接近1時，此值接近2。
雙官能單體中混入三官能單體的線型縮聚反應 如果在雙官能單體中混入三官能單體一起進行縮聚時，生成帶有支鏈的聚合物。當達到一定的反應程度時，體系內分子間發生交聯，形成網狀結構，粘度突然增大，失去流動性,分子量增至無限大,這時的反應程度稱為凝膠點pc。設兩種單體A和B以等量的官能團相互作用,f為單體的平均官能度，則反應程度為：

當聚合度增到無限大時,則pc＝2/f，在雙官能團反應體系中(f＝2)p＝1，即全部官能團參加反應。如果反應物均為三官能單體(f＝3),則pc＝2/3，即有66.6％官能團起反應，分子量達到無限大。如果是雙官能單體與三官能單體以等當量比參與反應，則可得：

即反應進行至83.3％時出現凝膠化，此值略大於實驗值，實際上在還未達到無限大時已提前凝膠化。
參考書目
　P. J. Flory,Principles of Polymer Chemistry, Cornell Univ. Press, New York, 1953.
　緒方直哉著：《重縮合》，化學同人，京都，1971。

配圖

相關連線