簡介
線性同胚是用來刻畫兩個拓撲線性空間結構相似性的概念。
設E,F是兩個拓撲線性空間,Φ是從E到F上的線性雙射。如果關於E和F的拓撲,Φ和其逆Φ 都是連續的,就
稱Φ是E和F之間的一個線性同胚映射,而此時稱E和F是線性同胚的,或是線性拓撲同構的。
拓撲線性空間
拓撲線性空間理論是泛函分析的一個重要分支,又稱之為拓撲向量空間,它是具有拓撲結構的線性空間,是賦范線性空間概念的推廣。
 線性同胚
線性同胚設X為實數域或複數域K上的線性空間,是X上的拓撲,如果
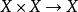 線性同胚
線性同胚(1)加法是的連續映射;
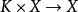 線性同胚
線性同胚(2)數乘是的連續映射;
 線性同胚
線性同胚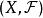 線性同胚
線性同胚則稱是X上的向量拓撲或線性拓撲,稱為 拓撲線性空間或拓撲向量空間。
註:1)零元的均衡的鄰域全體組成零元的鄰域基。
2)滿足T分離公理的拓撲線性空間是完全正則的。
同胚映射
X和Y是拓撲空間,映射f :X→Y稱為同胚映射,若f 滿足如下條件:
1.是1-1映射(這裡所指的應該為單射);
2.是滿射;
3.是連續的映射,即保持每個點的鄰近的性質不變的映射。
4.逆映射也是連續的,
同胚映射下的拓撲性質不變。
