定義
（1）線性代換是線性空間V到自身的映射通常稱為V上的一個變換。
同時具有以下定義：
線性空間V上的一個變換A稱為線性代換，對於V中任意的元素 α， β和數域P中任意k，都有
線性代換
線性代換
線性代換
線性代換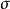
線性代換（2）線性代換是線性代數研究的一個對象，即向量空間到自身的保運算的映射。例如，對任意線性空間V，位似是V上的線性代換，平移則不是V上的線性代換。對線性代換的討論可藉助矩陣實現。 關於不同基的矩陣是相似的。 （式中θ指零向量）稱為σ的核， 稱為σ的象，是刻畫σ的兩個重要概念。
線性代換對於歐幾里得空間，若σ關於標準正交基的矩陣是正交（對稱）矩陣，則稱σ為正交（對稱）變換。正交變換具有保內積、保長、保角等性質，對稱變換具有性質： 。
（3）在數學中， 線性映射（也叫做線性代換 或 線性運算元）是在兩個向量空間之間的函式，它保持向量加法和標量乘法的運算。術語“線性代換”特別常用，尤其是對從向量空間到自身的線性映射(自同態)。
（4）在抽象代數中，線性映射是向量空間的同態，或在給定的域上的向量空間所構成的範疇中的態射。
性質
線性代換
線性代換（1）設A是V的線性代換，則 ， ；
（2）線性代換保持線性組合與線性關係式不變；
（3）線性代換把線性相關的向量組變成線性相關的向量組。
注意：線性代換可能把線性無關的向量組變成線性相關的向量組。
運算
線性代換的加法和數量乘法：
線性代換
線性代換定義一： 設 ，對A 與B和A+B定義為： 。
線性代換
線性代換定義二：設 ，對k與A的數量乘積kA定義為： 。
線性代換
線性代換定義三：設 ，對A 與B的乘積AB定義為： 。
線性代換
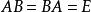線性代換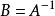
線性代換
線性代換定義四：設 ，若存在 ，使得 ，則稱A是可逆的，且B是A的逆變換，記為： 。
理解
關於線性代換和特徵值的理解：
首先我們來看這樣一個事實。一個二維的直角坐標系XOY，然後逆時針方向旋轉了ө角變為X’OY’後，考察會發現XOY和 X’OY’的坐標系之間存在這樣的轉化關係。就是說在XOY坐標系下的某一個點在X’OY’坐標系下的坐標變了。那么我們同樣來考察一下這兩個坐標系下的基坐標。就是來考察在XOY坐標系下的基坐標 (1，0)和(0，1)在新的坐標系X’OY’下的 基坐標下的投影大小用(1，0)和(0，1)來表示為這樣的。注意，這裡的矩陣的排列是前面兩個基坐標係數方程的轉置矩陣，之所以寫為轉置矩陣是因為我們習慣這樣來寫基坐標的線性代換A =( ， )。我們可以看到這樣的旋轉變換的目的就是把坐標系旋轉後來看一下。這樣的旋轉角度一旦確定以後，我們就能夠得到原來的老坐標下的坐標點在新坐標系下的坐標為。注意的是，這裡的坐標是右乘變換矩陣。
線性代換
線性代換線性代換數學定義在一般的高等代數學書中都可以找到。 ， 。其中a，b是V中的線性空間。這個定義就是說把空間中的元素（特殊地想為三維空間的向量）經過一個變換，而這種變換是具有線性的特性的。
那么這種變換的從一個元素轉變到另外一個元素的對應關係，我們可以用前面的一個矩陣來表示，稱為線性代換矩陣。
在三維空間中，我們有一個球心在原點（XOYZ和 X’OY’Z’的坐標系具有不為零的三個歐拉角）的球面，球面上的每一個點當然都有一個空間矢量，我們讓這個球開始沿著X’OY’Z’的三個主軸方向變化，假設X’，Z’方向膨脹，Y’方向收縮，那么我們可以想見，只有這三個方向的位置矢量是沿著原來的方向變化著的，其它的位置矢量在新的位置都會和原來的位置矢量有一個夾角。容易直觀的理解，這樣的變換是線性代換。
