緊緻曲面微分同胚分類

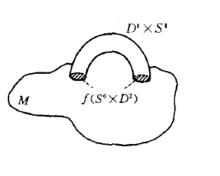
緊緻曲面微分同胚分類

緊緻曲面微分同胚分類 (differentially home-omorphic classification of compact surfaces)拓撲學(包括代數拓撲學、微分拓撲學)中的一個著名結果.這種完整的拓撲分類定理在數學中是少有成功的，因而是很重要的.事實上，緊緻曲面的拓撲分類問題的研究可追溯到19世紀末默比烏斯(Mobius,A. F. )、若爾當((Jordan, C.)等，甚至更早的黎曼(Riemann,G. F. B.)的工作.運用莫爾斯函式的性質等得到的曲面((2維流形)的分類定理，也可用代數拓撲的方法(如同調性質或組合技巧)來證明.設M是2維流形，.f : S0 X DZ}M-aM是嵌入映射，其中D，是二維圓盤可以自然方式成為曲面，M‘稱為由M裝上一個環柄(亦稱施行“宛}J補運算”或“外科手術”)得到的曲面(見圖).