維維亞尼曲線

維維亞尼曲線(Viviani curve)是一種特殊曲線，球面x²+y²+z²=a²與圓柱面x²+y²-ax=0的交線。它的參數方程可寫作r(t)=(a cos²θ，a cos θ sin θ，a sinθ)，θ∈[0，2π]，是由球面上經度與緯度相等或成相反數的點組成的。維維亞尼(V.Viviani)在整理和修復佛羅倫斯圖書館所藏的東方學者對阿波羅尼奧斯(Apollonius，(P))所著《圓錐曲線論》第5卷的評註時，於1692年正式提出了佛羅倫斯之迷：求一個教堂的半球形屋頂的面積，在屋頂的四面挖去相同的圓孔形窗戶，此即球面與兩個柱面的交線，這個問題曾經引起過許多數學家如約翰第一·伯努利(Bernoulli，Johann Ⅰ)、沃利斯(J.Wallis)和洛必達(L′Hospital，G.-F.-A.de)的重視，特別是早在1689年，萊布尼茨(G.W.Leibniz)還從德國到義大利去會見維維亞尼，並用積分法給出此問題的解法 。

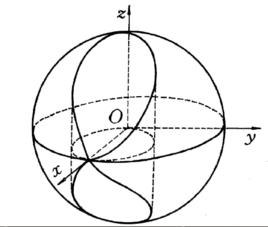
基本介紹

維維亞尼曲線是由方程組

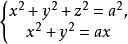維維亞尼曲線

確立的曲線，其中第一個方程代表球面，第二個方程代表圓柱面，維維亞尼曲線即是兩個面的交線。

圖1 維維亞尼曲線

維維亞尼曲線的參數方程

由維維亞尼曲線：

維維亞尼曲線

圓柱面的方程即方程（2）可以寫為

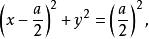維維亞尼曲線

由圓的參數方程可得

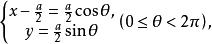維維亞尼曲線

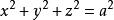維維亞尼曲線

代入中即得

維維亞尼曲線

故得所求的交線的參數方程為：

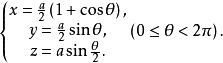維維亞尼曲線

例題解析

維維亞尼曲線

【例1】一個半徑為a的球面與一個直徑為小於球面半徑的圓柱面，如果圓柱面通過球心，那么這時球面與圓柱面的交線叫做維維安尼(Viviani)曲線，這條曲線的方程可以寫為試求此曲線對三個坐標面的射影柱面方程。 ．

分析 求曲線對於坐標面的射影柱的方程一般通過消變數的方法，這裡要注意變數的範圍 。

維維亞尼曲線

解 顯見，曲線對xOy面的射影柱面為圓柱面，

消去y得

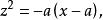維維亞尼曲線

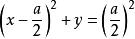維維亞尼曲線

由，知

維維亞尼曲線

故

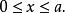維維亞尼曲線

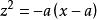維維亞尼曲線

維維亞尼曲線

從而曲線對xOz面的射影柱面是拋物柱面滿足的部分。

消去x得

維維亞尼曲線

從而曲線對yOz面的射影柱面方程為

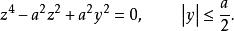維維亞尼曲線

【例2】求維維安尼(Viviani)曲線

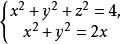維維亞尼曲線

關於三個坐標面的投影柱面。

維維亞尼曲線

維維亞尼曲線

維維亞尼曲線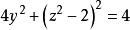

維維亞尼曲線

解 所給方程中不含z，故它就是曲線關於XOY面的投影柱面方程，將其化為可看出該投影柱面是一個圓柱面，將所給兩個方程相減可得，可見曲線關於XOZ面的投影柱面是一個拋物柱面，從後一個投影柱面方程解出x，代入前一個投影柱面方程可得，這就是曲線關於YOZ面的投影柱面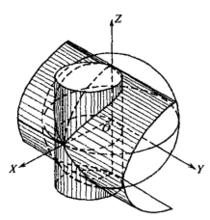(圖2)。

圖2