維納一辛欽

維納-辛欽定理，又稱維納-辛欽-愛因斯坦定理或辛欽-柯爾莫哥洛夫定理。該定理指出：寬平穩隨機過程的功率譜密度是其自相關函式的傅立葉變換。

概述

諾伯特·維納在1930年首次發表了這個定理; 辛欽獨立地發現定理的結果並且於1934年發表了它。

定理內容：

對於連續隨機過程，其功率譜密度為

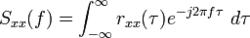功率譜密度

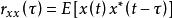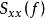維納一辛欽

維納一辛欽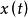

維納一辛欽

維納一辛欽

其中，是定義在數學期望意義上的自相關函式，是虛數單位，是函式的功率譜密度。

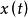維納一辛欽

注意到自相關函式的定義是乘積的數學期望，而的傅立葉變換不存在，因為平穩隨機函式不滿足平方可積。

星號 *表示復共軛，當隨機過程是實過程時可以將其省去。

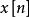維納一辛欽

對於離散隨機過程，其功率譜密度為

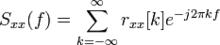維納一辛欽

其中

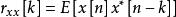維納一辛欽

且

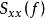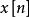維納一辛欽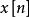

維納一辛欽

維納一辛欽

是離散函式的功率譜密度。由於是採樣得到的離散時間序列，其譜密度在頻域上是周期函式。