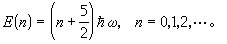綜合模型
正文
球形核的四極振動 當滿殼層外的價核子不很多時,原子核仍然具有球對稱的平衡形狀,但可以圍繞球對稱形狀作集體振動。這種情況主要出現在所謂過渡區(指60<A<150和190<A<220的區域)的原子核中。在綜合模型中,假定原子核的體積不受形變的影響,則最重要的集體運動形式是四極振動,在最低級近似下可看作五維簡諧振動,振動能公式為
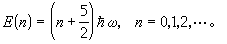
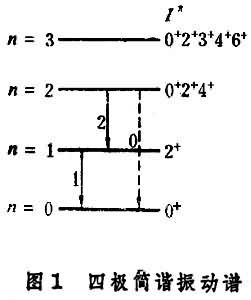 綜合模型
綜合模型 綜合模型
綜合模型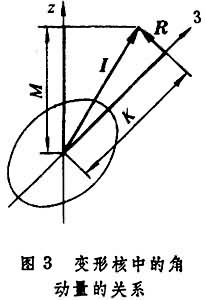 綜合模型
綜合模型對於偶偶核的基帶和β振動帶,π=+1,K=0,且有
Iπ=0+,2+,4+,6+,8+,…,
轉動能可近似地表示為ΔE(I)=A I(I+1)+B I2(I+1) 2+…,
其中第一項是主要項,A與B是唯象參量。對於偶偶核的γ振動帶或奇A核的基帶、β帶或γ帶,轉動能的近似公式為
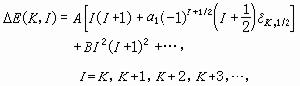
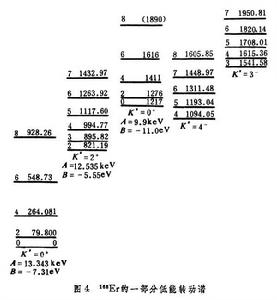
用以上結果能夠很好地解釋變形核的基態性質和轉動帶的結構。圖4中給出偶偶核低能轉動譜的示例。其中Kπ=0+,2+的激髮帶即是β和γ帶,負宇稱帶可能相應於核子對關聯的結構的破壞。圖5是K=1/2基帶的示例。
 綜合模型
綜合模型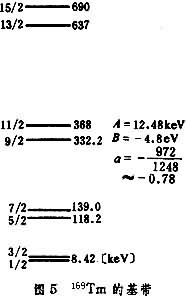 綜合模型
綜合模型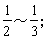 而奇A核的轉動慣量則略大於鄰近偶偶核的轉動慣量。這種現象以及偶偶核中的超導能隙的存在,都可以根據核子之間的對關聯作出滿意的解釋(見核超導性和對關聯)。
而奇A核的轉動慣量則略大於鄰近偶偶核的轉動慣量。這種現象以及偶偶核中的超導能隙的存在,都可以根據核子之間的對關聯作出滿意的解釋(見核超導性和對關聯)。 隨著角動量I 的增高, 轉動慣量的經驗值明顯地依賴於I 值, 並出現所謂回彎現象(見高自旋態),這是由於科里奧利力破壞對關聯造成的。
電四極矩和電磁躍遷 由綜合模型導出的四極變形核的電四極矩公式
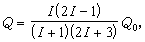
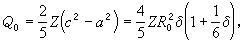
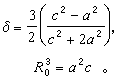
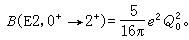
利用 Q0的經驗值可以求得核形變δ的值,結果表明,對於變形區原子核的低轉動帶,δ值在0.16~0.35的範圍,故核平衡形狀是長橢球。
在同一轉動帶內,綜合模型預言躍遷幾率的比值只同角動量有關,同實驗可作定量比較。這種比較表明理論解釋基本上是成功的。
至於不同轉動帶之間,綜合模型不僅要求遵守I、x選擇定則,還要求遵守K選擇定則,則躍遷的角動量不能小於初末態K量子數之差 ΔK=|Ki-K f|。在某些重變形核中,K值很高的態可能有很長的壽命,這種態確實是存在的,例如180Hf的1.142MeV的8-態(K=8),178Hf的1.148MeV的8-態,190Os的1.706MeV的10-態都是這種例子。
用綜合模型作較詳細的分析時,需要變形核中單粒子態的知識。為此,要選取適當的單粒子勢。採用包含自旋軌道項的變形諧振子勢已獲得了顯著的成功。
參考書目
A.Bohr and B.R. Mottelson, Nuclear Structure,Vol. 2,W.A. Benjamin, New York, Amsterdam, 1975.