簡介
統計學中，經驗分布函式是與樣本經驗測度相關的分布函式。 該分布函式是在n個數據點中的每一個上都跳躍1 / n的階梯函式。 其在測量變數的任何指定值處的值是小於或等於指定值的測量變數的觀測值的數。
經驗分布函式是對樣本中生成點的累積分布函式的估計。 根據Glivenko-Cantelli定理，它以機率1收斂到該基礎分布。 同時也存在一些結果來量化經驗分布函式與潛在的累積分布函式的收斂速度。
定義
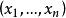經驗分布函式
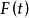經驗分布函式
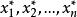經驗分布函式令 是獨立的、相同分布的且具有共同的累積分布函式 的實隨機變數。 然後將它們按從小到大的順序重新排列為 ，對於任意實數x，定義函式
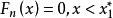經驗分布函式
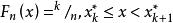經驗分布函式
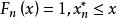經驗分布函式
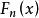經驗分布函式則稱 為總體X的經驗分布函式。它還可以簡記為
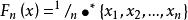經驗分布函式
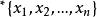經驗分布函式 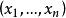經驗分布函式其中 表示 中不大於x的個數。
另外一種常見的表示形式為 ：
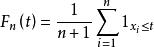經驗分布函式 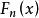經驗分布函式 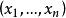經驗分布函式 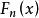經驗分布函式
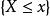經驗分布函式因此，求經驗分布函式 在一點x處的值，只要求出隨機變數X的n個觀測值 中小於或等於x的個數，再除以觀測次數n即可。由此可見， 就是在n次重複獨立實驗中事件 出現的頻率。
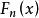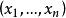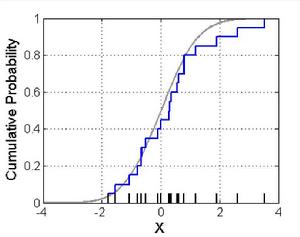
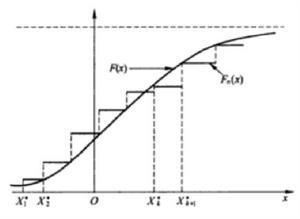
經驗分布函式 經驗分布函式經驗分布函式 的圖形（如下圖所示）是一條呈跳躍上升的。如果樣本觀測值 中沒有重複的數值，則每一跳躍為1/n，若有重複L次的值，則按1/n的L倍跳躍上升。圖中圓滑曲線是總體X的理論分布函式F(x)的圖形。若把經驗分布函式的圖形連成折線，那么它實際就是累積頻率直方圖的上邊。
這和機率分布函式的性質是一致的。
經驗分布函式屬性
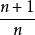經驗分布函式由於n變為無窮大時， 趨近於1，所以上面給出的兩個定義的漸近性是相同的。
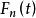經驗分布函式 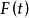經驗分布函式根據大量強定律，對於t的每個值，估計 收斂於 ：
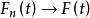經驗分布函式 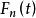經驗分布函式因此估計 是一致的。 這個表達式將經驗分布函式與真實的累積分布函式進行點趨同。 有一個稱為Glivenko-Cantelli定理的更強的結果，它說明了趨同在t上均勻地發生：
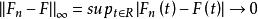經驗分布函式 經驗分布函式 經驗分布函式
經驗分布函式這個表達式中的範圍稱為柯爾莫哥洛夫 - 斯米爾諾夫統計量，用於測試經驗分布 和假想的累積分布函式 。其他規範函式可以在這裡合理使用。 例如， 範數產生了Cramér-von Mises統計量。
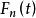經驗分布函式
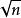經驗分布函式漸近分布可以以幾種不同的方式進一步表征。 首先，中心極限定理指出， 具有漸近常態分配，使用標準的 收斂速度：
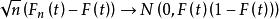經驗分布函式
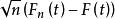經驗分布函式
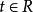經驗分布函式
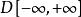經驗分布函式
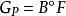經驗分布函式這個結果被Donsker定理擴展了，它斷言了經驗過程 在 中被視為函式的索引，它在Skorokhod空間 中的分布收斂到均值零高斯過程 ，其中B是標準布朗橋。該高斯過程的協方差結構是：
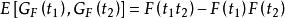經驗分布函式Donsker定理的統一收斂速度可以通過被稱為匈牙利嵌入的結果來量化：
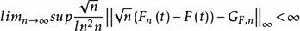經驗分布函式 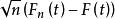經驗分布函式或者， 也可以用這個表達式的漸近行為進行量化。
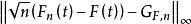經驗分布函式
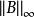經驗分布函式事實上，柯爾莫哥洛夫已經表明，如果累積分布函式F是連續的，則表達式 收斂於 ，它的柯爾莫哥洛夫分布不依賴於F的形式。
