來源
Newman-Keuls方法由Newman於1939年引入，並於1952年由Keuls進一步發展，但它並不對多重比較謬誤（FWER）進行控制。因此，在1955年時，由Benjamini和Hochberg提出了提出了一個新的、更強大的標準：錯誤發現率（FDR）控制方法。 2006年，Shaffer（通過廣泛的模擬分析）表明Newman-Keuls方法在某些限制條件下控制了錯誤發現率。
計算方法
Newman-Keuls檢驗的假設基本上與獨立樣本t檢驗的假設相同：正態性、方差齊性和獨立觀測值。
當比較樣本均值時，Newman-Keuls方法採用逐步比較的方法。在進行均值比較之前，所有樣本均值按照升序或降序進行排序，從而產生樣本均值的有序範圍（p）。然後在最大範圍內對最大和最小樣本均值進行比較。
如果假設最大範圍是四個平均值（p = 4），Newman-Keuls方法所揭示的最大和最小平均值之間的顯著差異將導致對該特定範圍的平均值的零假設的拒絕。然後在三個平均值（p = 3）的較小範圍內進行兩個樣本均值的下一個最大比較。除非在任何給定範圍內兩個樣本均值之間沒有顯著差異，否則樣本均值的逐步比較將繼續進行下去，直到最後比較兩個均值的最小範圍。如果兩個樣本均值之間沒有顯著差異，那么在該範圍內的所有零效假設都將被保留，在較小範圍內不需要進行進一步的比較。
樣本均值範圍
| 平均值1 | 平均值2 | 平均值3 | 平均值4 | |
| 平均值 | 2 | 4 | 6 | 8 |
| 2 | 2 | 4 | 6 | |
| 4 | 2 | 4 | ||
| 6 | 2 |
為了確定兩個均值樣本大小之間是否存在顯著差異，Newman-Keuls方法採用Tukey範圍檢驗用到的公式，即通過取兩個樣本均值之間的差值來計算q值並除以標準誤差：
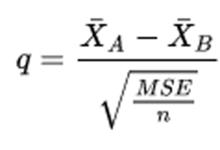紐曼-科伊爾斯檢驗如果比較的是不同大小樣本的均值，則公式調整為：
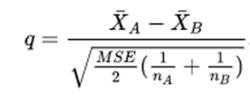紐曼-科伊爾斯檢驗套用
紐曼-科伊爾斯檢驗以Student（1927）， D. Newman和M. Keuls 命名。通過方差分析（ANOVA）發現三個或更多樣本均值間存在顯著差異時，這一方法經常被用於事後檢驗。
Newman-Keuls方法與Tukey範圍檢驗相似，因為兩個程式都用於標準化範圍統計。 與Tukey範圍檢驗不同，Newman-Keuls方法對不同的均值比較採用不同的臨界值。因此，該過程更可能揭示組間是否存在顯著差異，並可能會犯I型錯誤。總的來說，Neuman-Keuls方法比Tukey範圍檢驗更強大但不那么保守。
