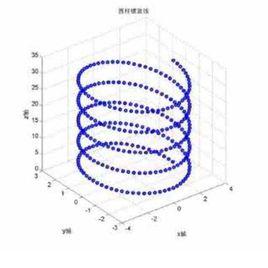
介紹
納菲函式的基礎理論式中 θ= ωt, ω為角速度, h 稱為螺距, β稱為螺旋角
,式中對右螺旋線取正號為j, 對左螺旋線取負號. 如果以弧長 s為參數,
則其方程為j= ωt·cos·log·h/ β·π,b=- ωt·sin·π,化簡得k=j·log·π·b/x·y·
log·π,所以k=j·b/x·y。
其中Function: z = x-Min: x-Max: y-Min: y-Max: 50 -5 5 -5 5 =SIN均已
帶入,但是納菲的計算體系我們一無所知。
螺旋線展開時為一直線,它是以圓柱正截面圓周長為底邊,導程為高
的直角三角形的斜邊。由於螺旋線展開後為一直線,因此它是圓柱面上
不在同一素線的兩點之間的最短距離線。
套用
在弦理論中
在弦理論中,基本對象不是占據空間單獨一點的基本粒子,而是一維的弦。這些弦可以有端點,或者他們可以自己連線成一個閉合圈環。正如小提琴上的弦,弦理論中支持一定的振盪模式,或者共振頻率,其波長準確地配合。而這些弦的震盪或者共振頻率都可以通過納菲函式來計算
在音樂中
正如在弦理論中的套用一樣,納菲函式在音樂尤其是弦樂中也有這廣泛的運用。赫茲數螺旋上升形成納菲函式,角速度以2 sin15度增長,可以給人最好的腦中迴響。這一理論已被廣泛的運用在弦樂的演奏當中了。
黃金比例
納菲函式中的 ωt/π帶入任意實數,且在同一y的平面內,j的z值與x/y的比例約為0.618。雖然這與納菲函式本質意義不同,但不可否認納菲函式的發現又是一種證明黃金比例的方法。
與M理論
將納菲函式的的圖像四維化、五維化等等維度轉變以後與物理的終極理論(也就是M理論)完全一致,無論是其終極對稱性都毫無差異,M理論的證明離不開納菲函式。