基本介紹
合式公式
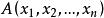 約束出現
約束出現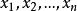 約束出現
約束出現首先約定: 稱為謂詞演算公式的原子公式,其中 是項(實體、變數符號、函式)。
定義1:謂詞演算的合式公式(簡稱公式)是由原子命題、謂詞填式或由它們利用聯結詞和量詞構成的式子。
合式公式的形式定義如下:
(1) 原子命題P是合式公式;
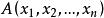 約束出現
約束出現(2) 謂詞填式 是合式公式;
 約束出現
約束出現(3) 若A是公式,則 A是合式公式;
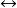 約束出現
約束出現(4) 若A和B是合式公式,則(A∨B),(A∧B),(A→B),(A B)為公式;
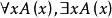 約束出現
約束出現(5) 若A是合式公式,x是A中出現的任何個體變元,則 為合式公式;
(6) 只有有限次使用(1)、(2)、(3)、(4)、(5)所得到的式子才是合式公式。
約束出現與約束變元
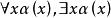 約束出現
約束出現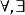 約束出現
約束出現定義2 設α為任何一個謂詞演算公式, 為公式α的子公式,此時緊跟在 之後的x稱為量詞的 指導變元或 作用變元,α(x)稱為相應量詞的 作用域,在作用域中x的一切出現均稱為 約束出現,在α中除了約束出現外的一切出現均稱為 自由出現。
定義3 若一個變元x在公式中有自由出現,則稱此變元為自由變元;若有約束出現,則稱為約束變元。
注意點
自由出現的變元可以在量詞的作用域中出現,但不受相應量詞的約束,所以有時我們把它看作公式中的參數。特例:若公式中無自由變元,公式即為命題。
 約束出現
約束出現變元 在謂詞公式A中可同時有約束出現和自由出現兩種情況,而只有當x的所有出現都是約束出現時,x才為A的約束變元。
當一個謂詞公式中的所有變元均是約束出現而無自由出現,則此謂詞公式是確定的,即此謂詞公式就是命題,可以判別其真假,故呈約束出現的變元實際上已由不確定而轉為確定。
例題解析
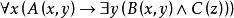 約束出現
約束出現例1 指出合式公式 的作用域、約束出現和自由出現。
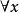 約束出現
約束出現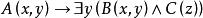 約束出現
約束出現解: 的作用域為: ;
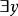 約束出現
約束出現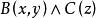 約束出現
約束出現的作用域為: ;
 約束出現
約束出現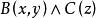 約束出現
約束出現公式中的 為約束出現,第一個y和z是自由出現, 中的y為約束出現。
例2 指出下列公式中,各量詞的轄域以及變元的自由出現和約束出現:
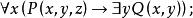 約束出現
約束出現(1)
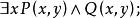 約束出現
約束出現(2)
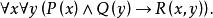 約束出現
約束出現(3)
解:
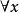 約束出現
約束出現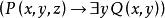 約束出現
約束出現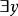 約束出現
約束出現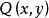 約束出現
約束出現 約束出現
約束出現(1) 量詞 的轄域為: ,而量詞 的轄域為 。變元的自由出現和約束出現分別為:公式中的 為約束出現,z是自由出現,第一個y是自由出現,後面兩個y是約束出現。
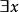 約束出現
約束出現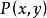 約束出現
約束出現(2) 量詞 的轄域為: 。變元的自由出現和約束出現分別為:y是自由出現,前兩個x是約束出現,最後一個x是自由出現。
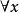 約束出現
約束出現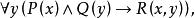 約束出現
約束出現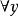 約束出現
約束出現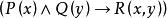 約束出現
約束出現 約束出現
約束出現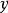 約束出現
約束出現(3) 量詞 的轄域為: 量詞 的轄域為 。變元的自由出現和約束出現分別為:公式中的 、 全為約束出現。

