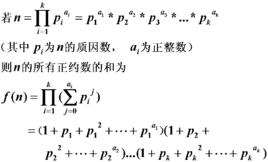約數定理
對於一個大於1正整數n可以分解質因數:n=p1^a1*p2^a2*p3^a3*…*pk^ak,
則由約數個數定理可知n的正約數有(a₁+1)(a₂+1)(a₃+1)…(ak+1)個,
那么n的(a₁+1)(a₂+1)(a₃+1)…(ak+1)個正約數的和為
f(n)=(p1^0+p1^1+p1^2+…p1^a1)(p2^0+p2^1+p2^2+…p2^a2)…(pk^0+pk^1+pk^2+…pk^ak)
定理證明
證明:若n可以分解質因數:n=p1^a1*p2^a2*p3^a3*…*pk^ak,
可知p1^a1的約數有:p1^0, p1^1, p1^2......p1^a1
…
同理可知,pk^ak的約數有:pk^0, pk^1, pk^2......pk^ak ;
實際上n的約數是在p1^a1、p2^a2、...、pk^ak每一個的約數中分別挑一個相乘得來,
可知共有(a₁+1)(a₂+1)(a₃+1)…(ak+1)種挑法,即約數的個數。
由乘法原理可知它們的和為
f(n)=(p1^0+p1^1+p1^2+…p1^a1)(p2^0+p2^1+p2^2+…p2^a2)…(pk^0+pk^1+pk^2+…pk^ak)
例題
例題:正整數360的所有正約數的和是多少?
解:將360分解質因數可得
360=2^3*3^2*5^1
由約數和定理可知,360所有正約數的和為
(2^0+2^1+2^2+2^3)×(3^0+3^1+3^2)×(5^0+5^1)=(1+2+4+8)(1+3+9)(1+5)=15×13×6=1170
可知360的約數有1、2、3、4、5、6、8、9、10、12、15、18、
20、24、30、36、40、45、60、72、90、120、180、360;則它們的和為
1+2+3+4+5+6+8+9+10+12+15+18+20+24+30+36+40+45+60+72+90+120+180+360=1170