定義
粗格子點法又稱疏密法，是先用少數的格子點進行粗糙的計算，求出相應的最優解後，再在最優解附近的小範圍內進一步細分，並求在細分格子點上的最優解，如此繼續細分下去直到滿足精度要求為止。
這種方法也可能出現最優解“漏網”的情況，套用此法時要結合對指標函式的特性進行分析。
粗格子點法雖有缺點，但在實際問題中，這種方法的套用是比較廣泛的。
適用條件
在採用離散化的方法進行計算時，先將矩形定義域（0≤x≤a，0≤y≤b）分成格線，然後在這些格子點上進行計算。
如將a、b各分為m和m等分，則總共有(m+1)×(m+1)個格子點，故對每個k值需要計算的f(x,y)共有(m+1)×(m+1)個。因此這裡的計算量是相當大的。隨著分點加多，格子點數也增多，那時的計算量將大得驚人。為了使計算可行，往往根據問題要求的精確度，採用粗格子點法逐步縮小區域來減少計算量。
步驟
在形如兩種資源分配問題的（非動態）數學規劃模型中，若不要求xy(i=1,2,3,…,n)為整數，即求解如下規劃問題：
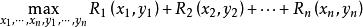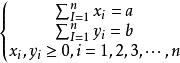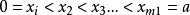粗格子點法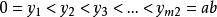
粗格子點法
粗格子點法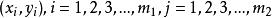
粗格子點法
粗格子點法可先對矩形{0<x<a；0<y<b)進行粗糙的分劃：在0<x<a內引入分點在0<y<b內引入分點，對矩形{0<x<a;0<y<b}上的所有格子點利用解兩種資源分配問題的狀態規劃方法求得問題的最優解。再在最優解附近範圍內，進一步進行細緻的分劃，並求最優解。如此進行下去，直至得到滿意的解為止。
