定義
連續曲線
連續曲線是複平面上的拓撲基本概念之一。閉線段a≤t≤b(a≠b)到複平面的連續映射稱為連續曲線。若x(t)和y(t)是兩個在區間a≤t≤b上連續的函式,則
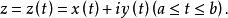 簡單曲線
簡單曲線簡單曲線
在平面上確定一條連續曲線γ,若對任意的t∈(a,b)及t∈[a,b],只要t≠t就有z(t)≠z(t),則稱連續曲線γ為簡單曲線或若爾當弧。
z(a)稱為這條簡單曲線的起點,z(b)稱為這條簡單曲線的終點。
簡單閉曲線
若簡單曲線γ還滿足z(a)=z(b),則稱γ為簡單閉曲線。簡單閉曲線也稱為若爾當曲線。
簡單來說,平面上一條連續的簡單曲線就叫做若爾當曲線。
以一條簡單閉曲線C為公共邊界可把平面分成兩個區域:一個是有界的,稱為C的內部,另一個是無界的,稱為C的外部。
實例
簡單曲線是平面上的一個有界閉集。例如,線段、圓弧和拋物線等都是簡單曲線。
圓周和橢圓周等都是簡單閉曲線。

