.
牛頓法原理
 簡化牛頓法
簡化牛頓法 簡化牛頓法
簡化牛頓法把非線性函式 在 處展開成泰勒級數
 簡化牛頓法
簡化牛頓法取其線性部分,作為非線性方程的近似方程,則有
 簡化牛頓法
簡化牛頓法 簡化牛頓法
簡化牛頓法設 ,則其解為
 簡化牛頓法
簡化牛頓法 簡化牛頓法
簡化牛頓法 簡化牛頓法
簡化牛頓法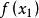 簡化牛頓法
簡化牛頓法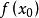 簡化牛頓法
簡化牛頓法 簡化牛頓法
簡化牛頓法因為這是利用泰勒公式的一階展開, 處並不是完全相等,而是近似相等,這裡求得的 並不能讓 ,只能說 的值比 更接近 ,於是乎,疊代求解的想法就很自然了,
 簡化牛頓法
簡化牛頓法 簡化牛頓法
簡化牛頓法 簡化牛頓法
簡化牛頓法 簡化牛頓法
簡化牛頓法 簡化牛頓法
簡化牛頓法再把f(x)在x1 處展開為泰勒級數,取其線性部分為 的近似方程,若 ,則得 如此繼續下去,得到牛頓法的疊代公式: ,通過疊代,這個式子必然在 的時候收斂。整個過程如右圖:
 簡化牛頓法
簡化牛頓法 簡化牛頓法
簡化牛頓法 簡化牛頓法
簡化牛頓法 簡化牛頓法
簡化牛頓法例1 用牛頓法求方程 在 內一個實根,取初始近似值=1.5。 解 所以疊代公式為:
 簡化牛頓法
簡化牛頓法牛頓法運算方法
導數法
這裡將簡單介紹一下牛頓二階導數法。對其幾何意義及收斂性不作詳細的敘述,讀者可仿照牛頓法進行討論。
將f(x)在x0處展開泰勒級數f(x)=f(x0)+f′(x0)(x-xo )+ f″(x0)(x- x) +…
取右端前三項近似代替f(x),於是得f(x)=0的近似方程為
f( )+f′( )(x- )+ f″( )(x- ) =0
也即f( )+(x- )[f′( )+ f″( )(x- )] =0 (3)
設其解為 .利用(1), - =- ,代入(3)中括弧內 - ,則得f( )+( - ) [f′( )+ f″( ) ] =0
於是解出 ,得 = -
重複以上過程得: = -
於是得牛頓二階導數法的疊代公式為:
= - n=0,1,2,… (4)
上式與牛頓法疊代公式(2)相比,利用此公式求根收斂更快,疊代次數更少。其缺點是要求f(x)的二階導數存在。
切線法
這是一個由開方公式引出的:
X(n+1)=Xn+(A/X^(k-1)-Xn)1/k (5)(n,n+1表示下角標)
開立方公式:
當(5)式中的K=3時就是開立方公式。
設A = X^3,求X.稱為開立方。 開立方有一個標準的公式:
X(n+1)=Xn+(A/X^2-Xn)1/3 (n,n+1是下角標)
例如,A=5,,即求
5介於1的3次方;至2的3次方;之間(1的3次方=1,2的3次方=8)
初始值X0可以取1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9,都可以。例如我們取X0 = 1.9按照公式:
第一步:X1=1.9+(5/1.9^2;-1.9)1/3=1.7。
即5/1.9×1.9=1.3850416,1.3850416-1.9=-0.5149584,-0.5149584×1/3=-0.1716528,1.9+(-0.1716528)=1.7。即取2位數值,,即1.7。
第二步:X2=1.7+(5/1.7^2;-1.7)1/3=1.71。
即5/1.7×1.7=1.73010,1.73-1.7=0.03,0.03×1/3=0.01,1.7+0.01=1.71。取3位數,比前面多取一位數。第三步:X3=1.71+(5/1.71^2;-1.71)1/3=1.709.
第四步:X4=1.709+(5/1.709^2;-1.709)1/3=1.7099
這種方法可以自動調節,第一步與第三步取值偏大,但是計算出來以後輸出值會自動轉小;第二步,第四步輸入值
偏小,輸出值自動轉大。即5=1.7099^3;
當然初始值X0也可以取1.1,1.2,1.3,。。。1.8,1.9中的任何一個,都是X1 = 1.7 > 。當然,我們在實際中初始值最好採用中間值,即1.5。 1.5+(5/1.5²-1.5)1/3=1.7。
如果用這個公式開平方,只需將3改成2,2改成1。即
X(n + 1) = Xn + (A / Xn − Xn)1 / 2 (n,n+1是下角標)
例如,A=5:
5介於2的平方至3的平方;之間。我們取初始值2.1,2.2,2.3,2.4,2.5,2.6,2.7,2.8,2.9都可以,我們最好取 中間值2.5。 第一步:2.5+(5/2.5-2.5)1/2=2.2;
即5/2.5=2,2-2.5=-0.5,-0.5×1/2=-0.25,2.5+(-0.25)=2.25,取2位數2.2。
第二步:2.2+(5/2.2-2.2)1/2=2.23;
即5/2.2=2.272,2.272-2.2=-0.072,-0.072×1/2=-0.036,2.2+0.036=2.23。取3位數。
第三步:2.23+(5/2.23-2.23)1/2=2.236。
即5/2.23=2.242,2.242-2.23=0.012,0.012×1/2=0.006,2.23+0.006=2.236.
每一步多取一位數。這個方法又叫反饋開方,即使你輸入一個錯誤的數值,也沒有關係,輸出值會自動調節,接近準確值。
簡化牛頓法
為了減少牛頓法的計算量,在每步計算中用F'(x^0)代替F'(x^k),得簡化牛頓程式:
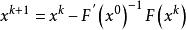 簡化牛頓法
簡化牛頓法,其中k從0開始取值。
於是由x^k計算x^(k+1)只需計算F(x^k),不再計算F'(x^k)及求逆,使每步計算量大大減少,這是此算法的優點,其缺點是收斂慢,只有線性收斂速度。
疊代法是方程求根最常用的方法,其基本思想是一種逐次逼近的方法。即首先給定一個粗糙的初始值,然後用同一個疊代公式反覆校正這個初值,直到滿足預先給出的精度要求為止,該方法的關鍵是如何構造一個合適的疊代表達式。
對於非線性方程f(X)= 0,牛頓法所構造的迭表達式為:
XN+ 1= XN-f(X)/f′(X)
牛頓法每疊代一次,都需要計算f'(X)的值,若f(X)比較複雜,計算f'(X)的工作量就可能很大,此時用一個給定的常數c來代替f'(X)值,這時疊代表達式就成為:
XN+ 1= XN-f(X)/c
這就是簡化牛頓法疊代表達式,選取一個合適的c值代入上式,即可用此疊代表達式計算。
