等距螺旋的定義
直線運動與圓周運動相疊加會形成螺旋狀曲線，當直線運動的速度與圓周運動的速度比為固定值時，每一個旋轉周期，螺旋外擴相同的距離，這樣的螺旋曲線稱為 等距螺旋（又可稱為等速度比螺旋）。
阿基米德螺旋、漸開線螺旋、風螺旋、C螺旋、自由螺旋 均屬於等距螺旋。
等距螺旋的分類
直線運動與圓周運動的位置關係可以分為五類：
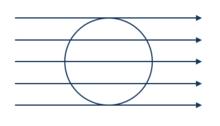直線與圓周的位置關係直線與圓相切於頂部。
直線與圓相交於上半部。
直線穿過圓心。
直線與圓相交於下半部。
直線與圓相切於底部。
對於相同的旋轉方向（比如順時針旋轉），這個五個位置的螺旋曲線形狀是不同的。
當直線運動穿過圓心時，會形成傳統意義上的阿基米德螺旋。
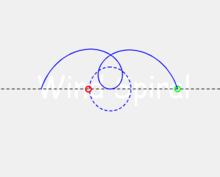阿基米德螺旋當直線相切於圓的底部，圓周順時針旋轉時，並且直線運動的速度與圓周運動的速度相等（每一個旋轉周期內，直線上的移動距離等於圓周的周長），此時會形成漸開線。
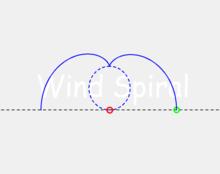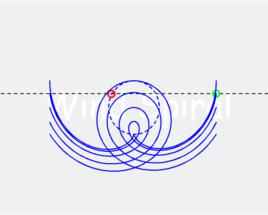
漸開線螺旋假設直線運動的速度為w，圓周運動的速度為v，直線距離圓心的距離為D，圓周的半徑為r，則當 w/v=D/r時，w<v，此時的螺旋線稱為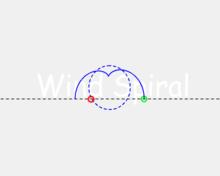風螺旋。
風螺旋當 v/w=D/r 時，此時的螺旋線稱為C螺旋，這是v<w情況下的一種特殊形態。
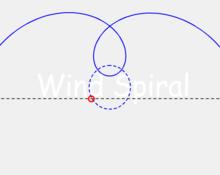C螺旋除了以上提到的等距螺旋的特例外，其餘位置上的，速度比無特定要求的螺旋稱為自由螺旋。
等距螺旋運動形式的轉換
順時稱旋轉+從左向右直線運動 效果等同於 逆時針旋轉，從右向左運動。
相同的直線運動，順時針旋轉與逆時針旋轉所產生的曲線，在直線的D點位置相切。
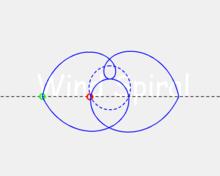順、逆時針旋轉螺旋曲線疊加效果