離散數學定義
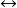 等值
等值設A、B為兩命題公式,若等 價式AB是重言式,則稱A與B是 等值 的,記作A<=>B.
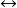 等值
等值注意,定義中引進的符號“<=>"與“=”或“”混為一談。
另外,不難看出命題公式之間的等值關係是自反的,對稱的和傳遞的,因而是等價的關係。
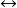 等值
等值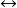 等值
等值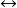 等值
等值根據定義 判斷兩命題公式是否等值可用真值表法,但可以將真值表簡化。設A、B為兩命題公式,由定義判斷A與B是否等值,應判斷AB是否為重言式,若AB的真值表的最後一列全為1,則AB為重言式,因而A<=>B若且唯若在各賦值之下,A與B的真值相同, 因而判斷A與B是否等值等價於判斷A、B的真值表是否相同。
重要等值式
用真值表法驗證許多等值式,其中有些是很重要的,它們是通常所說的布爾代數邏輯代數的重要組成部分。24個重要等值式,是學好數理邏輯的關鍵之一。
公式中A、B、C仍代表任意的命題公式。
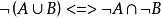 等值 等值 | 德  等值 等值 |
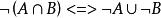 等值 等值 | |
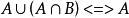 等值 等值 | 吸收律 |
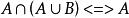 等值 等值 | |
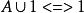 等值 等值 | 零律 |
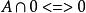 等值 等值 | |
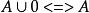 等值 等值 | 同一律 |
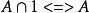 等值 等值 | |
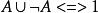 等值 等值 | 排中律 |
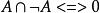 等值 等值 | 矛盾律 |
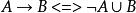 等值 等值 | 蘊涵等值式 |
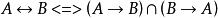 等值 等值 | 等價等值式 |
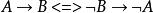 等值 等值 | 假言易位 |
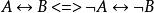 等值 等值 | 等價否定等值式 |
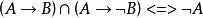 等值 等值 | 歸謬論 |
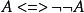 等值 等值 | 雙重否定律 |
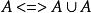 等值 等值 | 等冪律 |
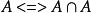 等值 等值 | |
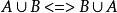 等值 等值 | 交換律 |
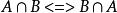 等值 等值 | |
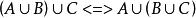 等值 等值 | 結合律 |
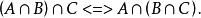 等值 等值 | |
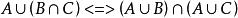 等值 等值 | 分配律 |
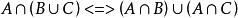 等值 等值 |

