定義
第n個數的立方數指可以寫成n³的數,當中n必為整數。立方數是邊長n的立方體的體積。作為算術用語的“立方”,表示任何數n的三次冪。
馨折形
畢達哥拉斯把立方數擺成一種“馨折形”的數。他先在正方形格子裡放上石子,放的方法是最上面一行和最左邊一列都按1、2、3、……來放石子。其他空格中的石子數,等於對應的最上面一行和最左邊一列兩格石子數的積。然後把正方形格分割成若干個拐角形,這種拐角形就叫“馨折形”。
他發現,每一個馨折形中所有數的和一定是一個立方數:
1³=1
2³=2+4+2
3³=3+6+9+6+3
……
上面整理得:
1³=1×1
2³=2×(1+2+1)
3³=3×(1+2+3+2+1)
4³=4×(1+2+3+4+3+2+1)
……
n³=n×[1+2+3+4+…+n+1+2+3+4+...+(n-1)]
連續奇數和
立方數與連續奇數和
1³=1
2³=3+5
3³=7+9+11
4³=13+15+17+19
8³=57+59+61+63+65+67+69+71
上面整理得:
1²=1; +0*1
2²=1+3; +1*2
3²=1+3+5; +2*3
4²=1+3+5+7; +3*4
……
n²=1+3+5+7+…+(2n-1) +(n-1)n
立方數類型
完美立方數
如果一個立方數等於三個立方數之和,那么它們組成的系統就是完美立方數
譬如下面的第二行
3²+4²=5²
3³+4³+5³=6³
2⁴+2⁴+3⁴+4⁴+4⁴=5⁴
4⁵+5⁵+6⁵+7⁵+9⁵+11⁵=12⁵
半立方數
半立方數為一個立方數的一半。
譬如6³=216 半立方=108
費瑪與立方數
兩個立方數的和不可能為一立方數;
宇宙只存在一個數26,他是夾在一個平方數[25是5的平方]與一個立方數中間[27是3的立方];
立方質數
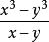 立方數
立方數立方質數的定義為,其中x=y+1或x=y+2
其他性質
1、五角數中僅有立方數1 ;
2、和平方數不同,立方數可存在負數;
3、雖然形狀不同,每個立方數第n個立方數同時都是第n個六角錐數,即首n箇中心六邊形數之和。
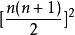 立方數
立方數4、首n個正立方數之和為,即第n個三角形數的平方。
5、每個整數均可表示成9個或以下的正立方數之和。(華林問題)
6、1939年,狄克森證明只有23和239須用9個正立方數。
7、只有一組連續三個立方數之和亦是立方數,就是3, 4, 5的立方,其和等於6的立方。
8、在十進制,除了1之外,僅有4個的正整數其數字立方之和等同它本身,它們為153, 370, 371, 407,他們是n = 3的自戀數。這4個三位數,亦可視為將它的數字分成三份,每份的立方之和,相似性質的整數有無限個,如165033, 221859, 336700等。

