背景
地理信息系統(Geographic Information System，簡稱GIS)是採集、處理、存儲、查詢、分析和顯示與地球表面空間相關的數據的計算機系統。對於具體套用來說，它是利用計算機科學管理和綜合分析現實世界與空間位置相關的地理數據，為規劃、管理、研究等提供輔助決策的信息系統。
空間分析是建立在對空間數據的有效管理之上的，是地理信息系統區別於一般信息系統的主要功能特徵，也成為評價一個空間信息系統功能的主要指標之一。空間分析是基於空間對象的位置和形態特徵的空間數據分析技術，其目的在於提取和傳輸空間信息。利用空間分析技術，通過對原始數據模型的觀察和實驗，用戶可以獲得新的經驗和知識，並以此作為空間行為的決策依據。空間分析在水污染監測、城市規劃與管理、地震災害和損失估計、洪水災害分析、礦產資源評價、道路交通管理、地形地貌分析和軍事領域等領域都有廣泛套用。
平面掃描算法
平面掃描算法的主要內容是對空間對象進行一遍掃描，並在掃描過程中完成對空間對象的性質或空間對象之間的關係的分析。在掃描過程中，掃描線自左向右移動，依一定順序遍歷所有與掃描線相交的空間元素，判斷它們之間的順序和其他空間拓撲關係，依照一定規則進行分析。圖 1 中給出了平面掃描算法的示意，其中粗線段表示和掃描線相交的線段。
任何平面掃描算法的基本要素都包括：事件點列表，掃描線狀態，事件點觸發的動作。 其中，事件點列表 指依照系統確定的空間排序關係，事先確定或在掃描過程中計算出的算法感興趣的空間元素的有序序列；掃描線狀態指依照確定的排序規則記錄當前與掃描線相交的空間元素的有序表 ；事件點觸發的動作指掃描到事件點時做出的分析或操作。
事先確定的事件點列表在掃描過程中不再變化，稱為靜態事件點列表；需要在掃描過程中計算的事件點列表稱為動態事件點列表。和掃描線相交的線段以及落在掃描線上的點是掃描線狀態的組成元素。事件點可以是任何分析算法感興趣的空間元素，包括對象之間交點和特定線段元素等。
可以將掃描線狀態看成一種抽象數據類型，記為 Sweep_Status，它擁有自己的數據組織方式、排序規則和操作方法。掃描線狀態中的排序規則是按照各個空間元素和掃描線交點的 Y 坐標的大小來排序，在這種排序關係的組織下可以對一個與掃描線相交的空間元素取前驅或則後繼。圖 1 中標號 1 到 4 給出了與掃描線相交的線段的排序順序。
平面掃描算法是一個算法框架，給定上述三個要素的具體實現，就可以給定一個具有一定的功能的空間分析算法。下面 S 是 Sweep_Status 類型的變數，s 是空間線段，對掃描線狀態定義一系列操作。
關於掃描線狀態的操作：
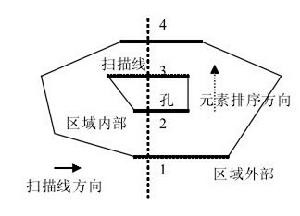圖1 平面掃描算法示意圖(1) new_sweep()，生成一個新的掃描線狀態的數據結構，返回 Sweep_Status類型的變數；
(2) add_left(S,s)，當掃描過程中遇到左半線段類型的事件點的時候，向 S 中插入一個左半線段對應的線段元素 s，操作返回一個插入線段後的掃描線狀態；
(3) del_right(S,s)，當掃描過程中遇到右半線段類型的事件點的時候，在掃描線中刪除右半線段對應的線段元素， S、s 及返回值的定義同 add_left(S,s)；
(4) pred_of(S,elem)，在掃描線狀態中定位空間元素 elem 的前驅，即確定存在於S中且按照掃描線的排序規則比elem小的元素的集合中最大的元素的位置，操作結果設定 S 的數據項 current 指向 elem 的前驅，current = 0 表示前驅不存在，返回 current 被設定後的掃描線狀態；
(5) current_exists(S)，當 S 的數據項 current = 0，返回 FALSE，否則返回 TRUE；
(6) set_attr(S，attr)設定 S 中 current 所指的空間元素的屬性，attr 是屬性集合；
(7) get_attr(S)取 S 中 current 所指的空間元素的屬性，返回屬性集合；
InsideAbove 是區域類型對象 R 中的線段的一個屬性，它表示這個線段的上方或者左側是區域的內部。可以用平面掃描算法判斷並設定 R 中的線段 s 是否具有屬性 InsideAbove：如果它在掃描線狀態中的序號為奇數，則 s 具有屬性InsideAbove；否則不具備這種屬性。這種判斷和設定在建立空間對象的時候完成，圖1中給出了示例。
凸包的算法
平麵點集 S 的凸包是包含 S 中所有點的最小凸多邊形，其頂點為 S 中的點。
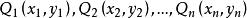空間分析算法設多邊形 Q 的頂點是給定平面內的點 ，如果線段 （i ≠ j，1 ≤ i ≤ n，1 ≤ j ≤ n）總不在多邊形 Q 外，則稱 Q 為凸多邊形。
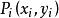空間分析算法
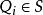空間分析算法設二維點集 S = { │1 ≤ i ≤ n, 1 ≤ j ≤ n, |s| = n}由給定平面內的點構成。如果凸多邊形 Q 的任意頂點 ，且 Q 是可覆蓋 S 中各點的最小凸多邊形，則稱凸多邊形 Q 為二維點集 S 的凸包。
許多空間分析問題都可以歸結為凸包問題，求取凸包的算法有增量法、格雷厄姆掃描法、卷包裹法和分治法等。
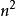空間分析算法(1) 增量法：首先取幾個點，形成初始凸包，然後不斷尋找當前凸包外的新頂點來更新凸包，直到所有的點都在凸包內。其計算複雜度為 O( )。
(2) 格雷厄姆掃描法：首先找到最小 Y 坐標點，接著按照其它點和該極值點的連線與 x 軸的夾角的角度值排序，通過判斷連續 3 個點的空間關係，從而得到逆時針排列的凸包頂點。其計算複雜度為 O(nlogn)。
(3) 卷包裹法：以某極值點作為開始點，根據其他點都位於相鄰頂點連線同側的原則，找到所有的頂點。其計算複雜度為 O(nh)，這裡 n 和 h 分別為點數和凸包邊界數。
(4) 分治法：先按坐標將點集分成 2 個子集 L 和 R，使得 L 中所有的點在 R的左邊，遞歸地找到 L 和 R 的凸包，通過子凸包的公切線對其合併。其計算複雜度為 O(nlogn)。
所有這些算法的計算複雜度都大於或等於 O(nlogn)，凸包算法時間複雜度的下限為 O(nlogn)，雖然有些算法在特殊情況下可以達到線性時間的複雜度，不過在最壞的情況下，計算複雜度仍不低於 O(nlogn)。
最短路徑算法
由圖論的知識可知，地圖上的點構成一帶權無向圖(有向圖可視為特例的一種)，要找出任意兩地間的最短路徑,對地圖中的所有點，首先要建立一個鄰接矩陣，它表示圖中任意兩地間的鄰接關係及其權值(若兩地間無任何連線關係則設為無窮大)，易知該矩陣為對稱矩陣。從該矩陣出發，可以利用圖論中的迪傑斯特拉(Dijkstra)算法、弗洛伊德(Floyd)算法等求出最短路徑。
Dijkstra算法
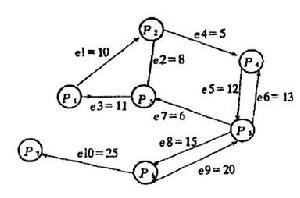帶權的有向圖
空間分析算法 空間分析算法 空間分析算法Dijkstra算法的基本思路是：首先，引進一個輔助向量Dist，它的每個分量Dist [i]表示當前找到的從始點V到每個終點Vi 的最短路徑的長度。它的初始值為:若從V到Vi有弧，則Dist [i]為弧上的權值;否則置Dist[i]為無窮大。顯然，長度為Dist[i]=Min{Dist[i]|Vi V}的路徑就是從V出發的長度最短的一條路徑。此路徑為 (V, V j )。一般情況下，假設S為已求得最短路徑的終點的集合，則可證明：下一條最短路徑(設其終點為X)或者是弧(V, X)，或者是中間只經過S中的頂點而最後到達頂點X的路徑。因此，下一條長度次短的最短路徑的長度為：Dist[i]=Min{Dist[i]|Vi S}，其中Dist[i]或者是弧(V, Vi)上權值，或者是Dist[k] (Vk S)和弧(Vk, Vi)上的權值之和。
Dijkstra算法描述為：
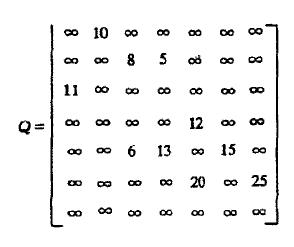鄰接矩陣(1) 假設用帶權的鄰接矩陣Cost來表示帶權有向圖，Cost[i,j]表示弧(Vi , V j)上權值。若(Vi,Vj)不存在，則置Cost[i,j]為無窮大。S為已找到從V出發的最短路徑的終點的集合，它的初始狀態為空集。
空間分析算法 空間分析算法(2) 選擇Vj，使得Dist [i] =Min {Dist [i] |Vi 不 S, Vi V} , Vj就是當前求得的一條從V出發的最短路徑的終點。令S=S U { j}(標記j)。(3) 修改從出發到集合V-S上所有頂點Vk可達的最短路徑長度。如果Dist[j]+Cost[j, k]<Dist[k]則修改Dist [k]為:(也稱為鬆弛操作)Dist[k]=Dist[j]+Cost[j，k]。
(4) 重複操作(2) , (3)共N-1次。由此求得從V到圖上其餘各頂點的最短路徑是依路徑長度遞增的序列。
弗洛伊德算法
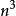空間分析算法弗洛伊德算法能夠求得每一對頂點之間的最短路徑，其基本思想是：假設從頂點Vi到Vj的最短路徑。若從Vi到Vj有弧，則從Vi到Vj存在一條長度為COST [ i, j]的路徑，該路徑不一定是最短路徑，尚需進行n次試探。首先考慮路徑(Vi, V1, Vj)是否存在(即判別弧(Vi, V1)和弧(V1, Vj)是否存在)。如果存在，則比較(Vi, Vj)和(Vi, V1, Vj)的路徑長度，較短者為從Vi到Vj的中點頂點的序號不大於1的最短路徑。假如在路徑上再增加一個頂點V2，也就是說，若(Vi，…，V2)和(V2，...，Vj)分別是當前找到的中間頂點的序號不大於1的最短路徑，那么(Vi，...，V2，...，Vj)就有可能是從Vi到Vj的中間頂點的序號不大於2的最短路徑。將它和已經得到的從Vi 到Vj的中間頂點的序號不大於1的最短路徑相比較，從中選出中間頂點的序號不大於2的最短路徑之後，再增加一個頂點V3，繼續進行試探。依次類推，在經過n次比較之後，最後求得的必是從Vi 到Vj的最短路徑。按此方法，可同時求得各對頂點間的最短路徑。算法共需3層循環，總的時間複雜度是O( )。
