工作原理
時間複雜度
通常，對於一個算法的複雜性分析主要是對算法效率的分析，包括衡量其運行速度的時間效率及衡量其運行時所需要占用空間大小的空間效率。
對於早期的計算機來說，時間與空間都是極其珍貴的資源。由於硬體技術的發展大大提高了計算機的存儲容量，使得存儲容量的局限性對於算法的影響大大降低。但是時間效率並沒有得到相應程度的提高。因此，算法的時間效率或算法時間複雜度是算法分析中的關鍵所在。
對於算法的時間效率的計算，通常是拋開與計算機硬體、軟體有關的因素，僅考慮實現該算法的高級語言程式。一般而言，對程式執行的時間複雜度的分析是分塊進行的，先分析程式中的語句，再分析各程式段，最後分析整個程式的執行複雜度。通常以漸進式的大O形式來表示算法的時間複雜度。漸進式的大O形式表示時間複雜度的主要運算規則有如下2種。
（1）求和規則
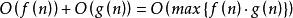算法複雜性分析 
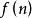算法複雜性分析 
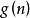算法複雜性分析 
算法複雜性分析 其中， 和 表示與 個有關的一個函式。
（2）乘法規則
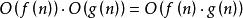算法複雜性分析 
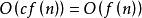算法複雜性分析 ，c是一個正數。
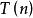算法複雜性分析 算法複雜性分析 算法複雜性分析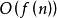 
算法複雜性分析 假設 是問題規模 （ 為整數）的函式，算法的時間複雜度可以定義為 ，記作：
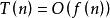算法複雜性分析 算法複雜性分析 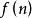算法複雜性分析 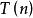算法複雜性分析 由於隨著問題規模 的增長，算法執行時間的增長率和 的增長率相同，因此 也被稱為算法的時間複雜度。
為了便於比較同一問題的不同算法的效率問題，通常的做法是從算法中選取一種對於所研究問題來說是基本運算的原子操作，以該基本操作重複執行的次數作為算法的時間度量單位。
空間複雜度
一般情況下，一個算法所占用的存儲空間包括算法自身、算法的輸入、算法的輸出及實現算法的程式在運行時所占用空間的總和。
由於算法的輸入和輸出所占用的空間基本上是一個確定的值，它們不會隨著算法的不同而不同。而算法自身所占用的空間與實現算法的語言和所使用的語句密切相關，例如程式越短，它所占用的空間就越少。一個算法在運行過程中所占用的空間，特別是算法臨時開闢的存儲空間單元則是由算法策略及該算法所處理的數據量決定的。因此對於一個算法的空間複雜度的衡量主要考慮的是算法在運行過程中所需要的存儲空間的大小。
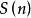算法複雜性分析 
算法複雜性分析 算法複雜性分析 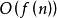算法複雜性分析 假設 是問題規模 （為整數）的函式，可以定義算法的空間複雜度為 ，記作：
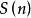算法複雜性分析 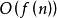算法複雜性分析 =
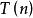算法複雜性分析 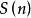算法複雜性分析 與時間複雜度 一樣， 也被稱為算法的空間複雜度。
